1. По двум независимым извлеченным из нормальных генеральных совокупностей выборкам, объемы которых n=9 и m=16, найдены исправленные выборочные дисперсии 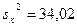 и
и 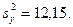 На уровне значимости 0,01 проверьте нулевую гипотезу
На уровне значимости 0,01 проверьте нулевую гипотезу 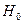 :
: 
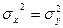 против конкурирующей гипотезы
против конкурирующей гипотезы 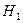 :
: 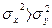 .
.
2. В партии из 500 деталей, изготовленных первым станком-автоматом, оказалось 60 нестандартных, из 600 деталей второго станка - 42 нестандартных. На уровне значимости 0,01 проверьте нулевую гипотезу 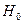 :
: 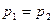 о равенстве вероятностей изготовления нестандартной детали обоими станками против конкурирующей гипотезы
о равенстве вероятностей изготовления нестандартной детали обоими станками против конкурирующей гипотезы 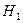 :
: 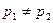 .
.
3. За последние 5 лет выборочная дисперсия доходности актива А составила 0,04, актива Б -0,05. Имеются ли основания утверждать, что вложения в актив А менее рискованны, чем в актив Б? Уровень значимости составил 5%.
4. За последние 7 лет выборочная дисперсия (исправленная) доходности актива А составила 0,05, актива Б -0,08. Имеются ли основания утверждать, что вложения в актив Б более рискованны, чем в актив А? Уровень значимости составил 5%.
5. По двум независимым, извлеченным из нормальных генеральных совокупностей выборкам, объемы которых n=50 и m=50 соответственно, найдены выборочные средние, равные 142 и 150 соответственно. Генеральные дисперсии известны: 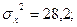
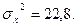 На уровне значимости 0,01 проверьте нулевую гипотезу
На уровне значимости 0,01 проверьте нулевую гипотезу 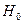 :
: 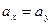 против конкурирующей гипотезы
против конкурирующей гипотезы 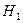 :
: 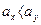 .
.
6. По двум независимым, извлеченным из нормальных генеральных совокупностей выборкам, объемы которых n=10 и m=10 соответственно, найдены выборочные средние, равные 14,3 и 12,2 соответственно. Генеральные дисперсии известны: 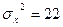 ,
, 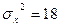 На уровне значимости 0,01 проверьте нулевую гипотезу
На уровне значимости 0,01 проверьте нулевую гипотезу 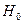 :
: 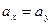 при конкурирующей гипотезе
при конкурирующей гипотезе 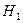 :
: 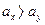 .
.
7. В селах Орехово и Шишкино проведены выборочные обследования доходов жителей. По выборкам из 10 человек получены следующие результаты: в Орехово –средний доход 2620 руб., среднее квадратическое отклонение 150 руб.; в Шишкино - средний доход 2380 руб., среднее квадратическое отклонение 90 руб. Можно ли утверждать на уровне значимости 10%, что в Шишкино живут в среднем беднее, чем в Орехово?
II. Независимые выборки.Пусть имеются две независимые выборки 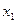 , , 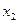 ,…, ,…, 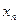 и и 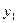 , , 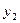 ,…, ,…, 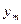 ,имеющие нормальное распределение с параметрами ,имеющие нормальное распределение с параметрами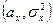 и и 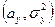 соответственно. Обычно формулируется задача проверки их однородности, то есть равенства обоих параметров, либоследует проверить равенство параметров по отдельности. В таблице представлены критерии проверки гипотез для независимых выборок. соответственно. Обычно формулируется задача проверки их однородности, то есть равенства обоих параметров, либоследует проверить равенство параметров по отдельности. В таблице представлены критерии проверки гипотез для независимых выборок.
Рассмотрите пример 2. По выборке объема n=30 найден средний вес изготовленных на первом станке изделий, равный 130 г.; по выборке объема m=40 найден средний вес изготовленных на втором станке изделий, равный 125 г. Генеральные дисперсии известны: Решение. Находим значение статистики критерия |
 2015-10-13
2015-10-13 4006
4006
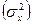 и
и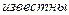 (для больших выборок, объемом порядка сотен)
(для больших выборок, объемом порядка сотен) 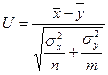
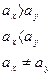
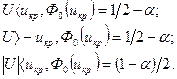
 но равны
но равны 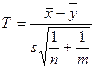
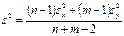
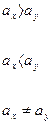
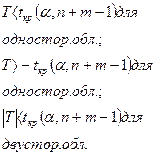
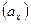 и
и 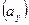
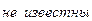
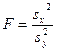 , где
, где 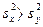
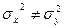
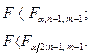

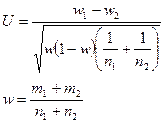
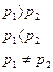
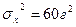 ,
, 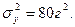 Проверьте на уровне значимости 0,05 нулевую гипотезу
Проверьте на уровне значимости 0,05 нулевую гипотезу 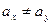 . Предполагается, что случайные величины распределены нормально и выборки независимы.
. Предполагается, что случайные величины распределены нормально и выборки независимы.
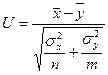 = 2,5. Из таблицы функции Лапласа находим критическую точку
= 2,5. Из таблицы функции Лапласа находим критическую точку 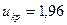 . Поскольку
. Поскольку 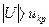 , то нулевая гипотеза отвергается. Ответ. Нельзя утверждать, что средние значения веса изделий двух станков совпадают.
, то нулевая гипотеза отвергается. Ответ. Нельзя утверждать, что средние значения веса изделий двух станков совпадают.






