Задание 15

а) Решите уравнение ;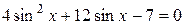

б) Найдите все корни данного уравнения, принадлежащие промежутку .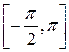

Задание 16. В правильной шестиугольной призме 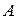,..., 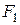все ребра равны 1.

1. Постройте сечение призмы плоскостью, проходящей через точк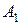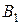и , и .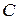

2. Найдите расстояние от точки 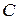до прямой .

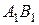Задание 17. Решите неравенство

.

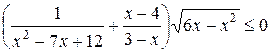Задача 18. Из вершины 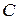тупого угла треугольника 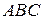проведена высота 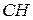. Точку 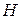соединили с серединам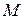и и 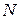сторон 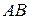и .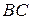

1. Докажите, что в четырехугольник 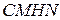можно вписать окружность.

2. Найти ее радиус, если сумма сторон 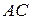и 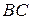равна 20, а площадь треугольника 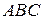равна 24.

Задание 19. 31 декабря 2013 года Андрей взял в банке некоторую сумму в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Андрей переводит в банк 3460600 руб. Какую сумму взял Андрей в банке, если он выплатил долг тремя равными платежами (то есть за 3 года).

Задание 20. Найти все значения параметра 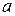, при каждом из которых среди значений функции 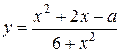есть ровно одно целое число.

Задание 21. На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно -5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно -18.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?