Основы теории зубчатого зацепления

Для обеспечения непрерывного зацепления двух тел с постоянным передаточным отношением их сопряженные поверхности должны быть очерчены по кривым, удовлетворяющим основному закону зацепления, который формулируется следующим образом: общая нормаль к сопряженным профилям, проведенная в точке их касания, делит меожосевое расстояние на части, обратно пропорциональные угловым скоростям.

Для доказательства сформулированной теоремы рассмотрим два зацепляю­щихся тела, вращающихся с постоянны­ми угловыми скоростями ω₁ и ω ₂ вокруг неподвижных осей О₁ и О₂ (рис. 7.2).

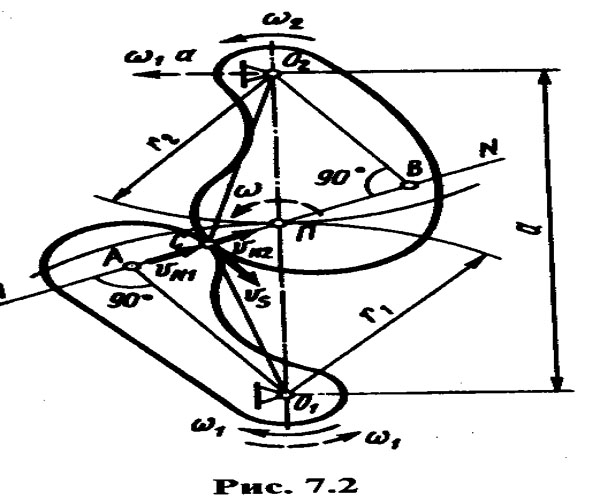
Для передачи силы давления одного тела на другое в точке С их контакта должна быть общая нормаль NN к со­пряженным профилям, которая пересечет линию центров О₁О₂ в точке П. Опустим перпендикуляры О₁А и О₂В из центров вращения на нормаль NN, а через точку П проведем две дуги окружности радиу­сов r₁ и r₂. Согласно законам вращательного движения, векторы скоростей точек С контакта двух тел перпендикулярны радиусам, проведенным из центров вращения в точку касания, и равны по модулю:

ν_C1= ω_1* О₁C. ν_C2= ω_2* О₂C

Разложим мысленно векторы скоростей точек С контакта двух тел на направление нормали и касательной к профилю; нормальные составляю­щие, согласно стандарту, обозначаются v_N1 и v_N2 и называются нормольной контактной скоростью (рис. 7.2), а касательные составляющие обозначаются v_A и v_B, и называются касательной контактной скоро­стью (на рис. 7.2 они не показаны).

Очевидно, что для непрерывного зацепления двух тел необходимо, чтобы

в противном случае первое тело должно внедряться во второе либо от­стать от него. Очевидно также, что абсолютные скорости v_A и v_B точек А и В направлены по нормали NN и эти скорости должны быть равны нормальной контактной скорости, т. е.

v_A= v_N1= v_N2= v_B

в противном случае произошло бы изменение размеров контактирующих тел.

Принимая во внимание, что треугольники АО₁П и ВО₂П подобны и что

v_A = ω₁ • АО₁ =v_B =ω₂ • BО₂, получим

Итак, для сохранения постоянного передаточного отношения и = ω₁/ω₂ = const точка П, называемая полюсом зацепления, должна со­хранять на линии центров постоянное положение и делить межосевое расстояние а в отношении r₁/r₂. Теорема доказана.

Основной закон зацепления имеет общий характер и справедлив также для случаев, когда передаточное отношение должно изменяться во времени, при этом полюс зацепления не остается непод­вижным, но будет перемещаться вдоль линии центров, а механизмы, осуществляющие подобное движение, имеют некруглые зубчатые колеса.

Окружности радиусов r₁ и r₂ проходящие через полюс, называются начальными; окружная скорость точек, лежащих на этих окружно­стях, одинакова и равна

ν = ω₁ r₁ = ω₂ r₂

Для рассмотрения относительного движения тел используем приме­няемый в теории механизмов и машин метод обращения дви­жений (метод остановки), т. е. сообщим всей системе вращение вокруг оси О₁ с угловой скоростью со, в направлении, противоположном перво­начальному (см. рис. 7.2). Тогда первое тело остановится, второе будет совершать сложное плоскопараллельное движение, состоящее из вращения вокруг осей О₁ и О₂ одновременно, а его движение по от­ношению к неподвижному первому телу можно рассматривать, при­меняя метод мгновенных центров скоростей, известный из теоретиче­ской механики.

Ранее мы установили, что окружные скорости точек, лежащих на на­чальных окружностях радиусов r₁ и r₂, всегда равны, следовательно, если первая окружность остановлена, то вторая будет катиться по первой без скольжения, а точка П станет мгновенным центром скоростей второго тела. Для определения мгновенной угловой скорости со запишем ско­рость оси О₂ в виде равенства:

v₀₂ = ω₁ a = ω₂ r₂

Так как а = r₁ + r₂. a ω₁ r₁ = ω₂ r₂

ω= ω₁ (r₁ + r₂) /r₂ = ω₁ r₁ /r₂ + ω₁, = ω₁ + ω₂.

Итак, после остановки первого тела второе будет вращаться вокруг полюса с мгновенной угловой скоростью ω = ω₁ + ω₂. Отсюда следует, что точка С контакта второго тела будет скользить по поверхности перво­го тела (см. рис. 7.2) со скоростью,

υ_s = ω • ПС = (ω₁+ω₂)ПС,

которая называется скоростью скольжения контактных точек. Скорость скольжения прямо пропорциональна расстоянию контактных точек от полюса. Скольжение контактных точек сопровождается трением.

Очевидно, что при зацеплении в полюсе скорость скольжения будет равна нулю, а после перехода точки контакта за полюс вектор скорости скольжения, как и сила трения, изменит направление на противоположное.

Требованиям основного закона зацепления удовлетворяют различные кривые, но наибольшее применение имеет эвольвентное зацепление, предложенное в середине XVIII в. Л. Эйлером; кроме того, в машино­строении применяется круговое зацепление, предложенное в 1954г. М. Л. Новиковым, а в приборостроении — циклоидальное и некоторые другие виды зацепления.

Свойства эвольвентного зацепления. Эвольвентой или раз­верткой окружности называют плоскую кривую, которая описывается любой точкой прямой NN, перекатываемой без скольжения по неподвиж­ной окружности (рис. 7.3). Линию .NN называют производящей прямой, а окружность диаметра d_b, по которой эта прямая перекатывается, — ос­новной окружностью. Так как перекатывание производящей прямой по основной окружности происходит без скольжения, то в каждый данный момент точка их касания является мгновенным центром скоростей и цен­тром кривизны эвольвенты, следовательно, производящая прямая в каждом своем положении будет нор­малью к эвольвенте, иначе говоря, нормаль эвольвенты всегда явля­ется касательной к основной ок­ружности.

.

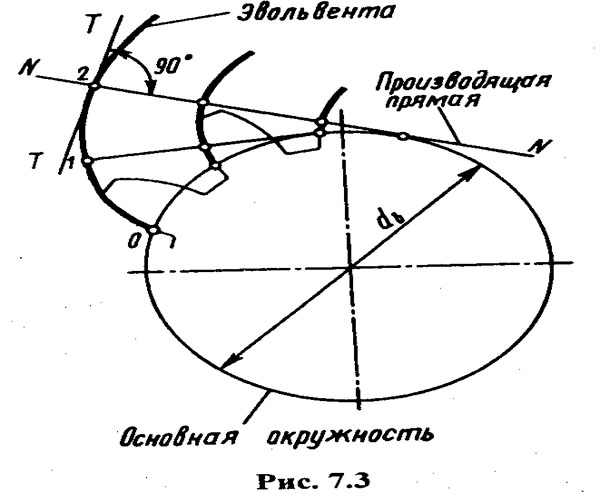
Из способа образования эволь­венты следует, что эта кривая не может существовать внутри ос­новной окружности. Если перекаты­вать производящую прямую в про­тивоположном направлении, то по­лучим другую ветвь эвольвенты — левую (эвольвенты, изображенные на рис. 7.3 жирной линией, пра­вые). Каждый зуб колеса с эвольвентным зацеплением очерчивает­ся участками правой и левой эвольвент рис 7.3форма зубьев внутри основной окружности опреде­ляется профилем зуборезного инструмента. Две одноименные (правые или левые) эвольвенты эквидистантные (равноудаленные) кривые, т. е. имеющие между собой одинаковое расстояние по любой общей нор­мали, равное длине дуги основной окружности между началом эвольвент.

Очевидно, что с увеличением диаметра d_b основной окружности ра­диусы кривизны эвольвенты будут увеличиваться, а в пределе при d_b→ ∞эвольвента обращается в прямую, следовательно, у рейки с эвольвентным зацеплением профиль зубьев должен быть прямолиней­ным. Именно поэтому в основу проектирования цилиндрических и кони­ческих зубчатых колес эвольвентного зацепления положены стандарт­ные исходные контуры, представляющие собой контур рейки с зубьями прямолинейного профиля (см. рис. 7.7).

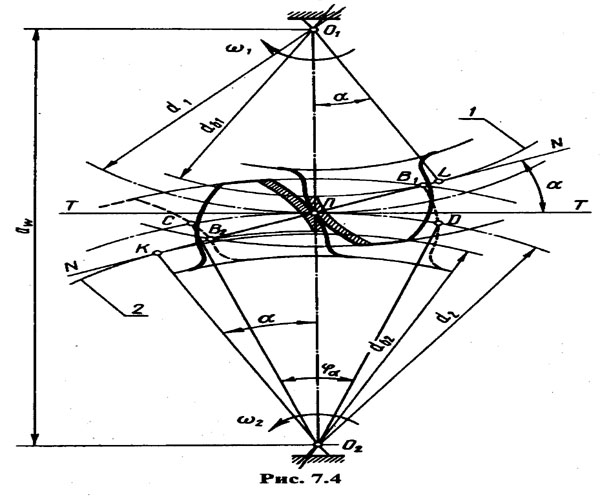
Рассмотрим (рис. 7.4) схему эвольвентного зацепления пары зубьев колес, вращающихся вокруг осей О₁ и О₂ с угловой скоростью ω₁ и ω₂ Положение полюса зацепления П определяется согласно основной теоре­ме зацепления, а общая нормаль NN к профилям зубьев в точке контакта — касательная к основным окружностям 1 и 2, диаметры которых в соответ­ствии со стандартом обозначены d_b1 и d_b2. Так как основные окружности имеют постоянный диаметр, то общая нормаль NN и полюс П будут за­нимать постоянное положение, следовательно, точка контакта зубьев перемещается по общей нормали, называемой поэтому линией зацепле­ния. Прямая линия зацепления присуща только эвольвентному зацеплению.

Угол α между линией зацепления NN и общей касательной ТТ к на­чальным окружностям называется углом зацепления; его стандартное зна­чение для эвольвентного зацепления α = 20°.

Если для той же пары колес немного изменить межосевое расстояние a_w то изменится угол зацепления α, но диаметры основных окружностей останутся неизменными.

Так как d_bl = d_b1cosα, d_b2 = d₂cosα (рис. 7.4), то передаточное от­ношение

u = 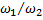= d₂/d₁ = d_b2/d_b1.

Таким образом, передаточное отношение эвольвентного зацепления зависит только от диаметров основных окружностей, следовательно, из­менение межосевого расстояния не влияет на кинематическую точ­ность эвольвентного зацепления, что является весьма существенным его

достоинством.

При изменении межосевого расстояния a_w окружности диаметров d₁ и d₂, перестанут касаться друг друга в полюсе П, т. е. появятся новые на­чальные окружности, которые будут проходить через полюс Я и в про­цессе зацепления перекатываться друг по другу без скольжения; поэтому окружности диаметров d₁ и d₂, не зависящие от межосевого расстояния, будем впредь называть делительными. Если межосевое расстояние пере­дачи точно равно полусумме диаметров делительных окружностей, то начальные и делительные окружности совпадают. Таким образом, на­чальная окружность — понятие кинематическое и для отдельно взятого зубчатого колеса не существует. Основные параметры зубчатого колеса определяются по делительной окружности.

Зуб колеса расположен между окружностью вершин зубьев и ок­ружностью впадин. Участок В₁В₂ линии зацепления NN (рис. 7.4), заклю­ченный между окружностями вершин зубьев, называется активной лини­ей зацепления. Часть профиля зуба, по которой происходит взаимодейст­вие с зубом парного колеса, называется активным профилем зуба (на рис. 7.4 активные профили отштрихованы).

Угол поворота колеса передачи от положения входа зуба в зацепле­ние до положения выхода из него называется углом перекрытия и обо­значается φ_γ (у косозубой передачи угол перекрытия (р₇ состоит из угла торцового перекрытия φ_α (см. рис. 7.4) _и угла осевого перекрытия φ_β).

Цен­тральный угол τ (см. рис. 7.6), рав­ный 2π/z или 360°/z (где z — число зубьев колеса), называется угловым шагом. Отношение угла пере­крытия колеса к его угловому шагу называется коэффициентом перекрытия передачи и обозначается ε, тогда

ε_у=φ_γ/π.

Для обеспечения непрерывности зацепления необходимо выполнить условие

φ_γ > π или ε_γ > 1,

иначе пара зубьев выйдет из зацепления раньше, чем войдет в зацепление следующая пара. Таким образом, если ε < 2, период зацепления одной пары зубьев состоит из периода однопарного и периода двупарного зацепления. Чем больше коэффициент перекрытия, тем меньше период однопарного зацепления; зацепление в полюсе всегда бу­дет однопарным.

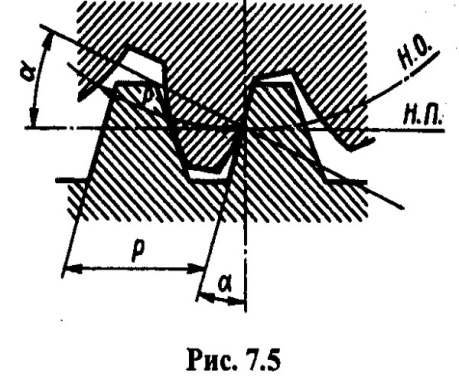
На рис. 7.5 изображено зацепление зубчатого колеса с рейкой, в ко­тором начальная окружность (Н.О.),колеса перекатывается без скольже­ния по начальной прямой (Н.П.) рейки. Угол профиля зуба рейки и угол зацепления, обозначенные α, равны между собой.2