Характеристики, обусловленные проявлением нелинейности УПТ

Нелинейность усилительного прибора или преобразователя частоты приводит к нелинейным искажениям в законе модуляции и к возникновению особых помех приема сигналов: перекрестных и интермодуляционных помех.

Процесс образования перекрестных и интермодуляционных помех демонстрируется на примере структурной схемы, состоящей из усилительного каскада (УК) и фильтра, настроенного на частоту основного канала 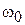(1.8).

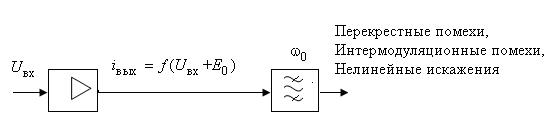
Рис. 1.8. Структурная схема УК и фильтра

На вход УК поступает аддитивная смесь

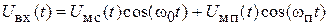(1.1)

полезного сигнала и помехи с частотой 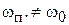. Помехой обычно является колебание на частоте соседнего канала приема. Усиление и нелинейные взаимодействия полезного сигнала и помехи происходят в УК. Фильтр выделяет колебания с частотой 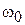. Сигнал и помеха являются амплитудно-модулированными колебаниями. Огибающи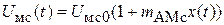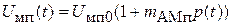е , , где 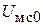- амплитуда полезного сигнала, 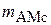- индекс амплитудной модуляции сигнала, 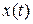- полезное сообщение, 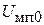амплитуда помехи, 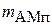- индекс амплитудной модуляции помехи, 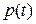- мешающее сообщение.

Передаточная характеристика усилительного прибора нелинейная и в общем виде представляется 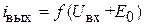. Так как уровень сигнала мал по сравнению со значением 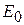в рабочей точке, то допустимо разложение в ряд Тейлора вблизи

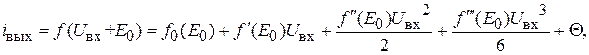(1.2)

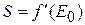– крутизна усилительного прибора. Из-за нелинейности УП 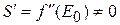и .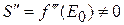

Из-за нелинейности передаточной характеристики усилительного прибора 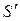и 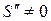при подаче на каскад суммы двух колебаний возникают гармоники сигнала и помехи и частоты 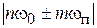. Из всех этих составляющих через полосовой фильтр пройдут только те, частота которых совпадает с частотой настройки фильтра.

Рассмотрим более подробно четвертое слагаемое в 1.2. При возведении в куб получается

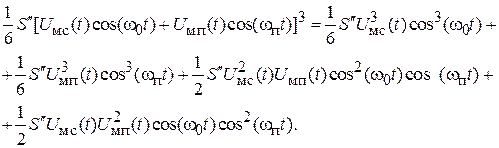
Тригонометрические преобразования с составляющими, которые могут образовать колебание с частотой 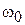, приводят к следующим выражениям:

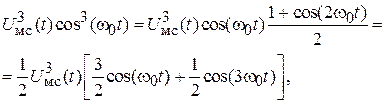
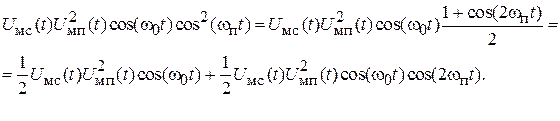
В полученных выражениях на частоте 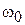присутствуют две составляющие: 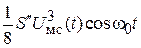и 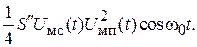Первая 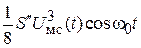представляет собой нелинейные искажения огибающей сигнала, так как перед 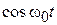стоит множитель 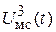, а вторая составляющая 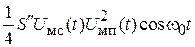является перекрестной помехой. Ее паразитная модуляция 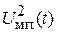перенеслась на несущее колебание 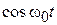, соответствующее полезному сигналу.

Общее выражение для амплитуды тока на частоте 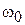с учетом усиления полезного сигнала имеет вид

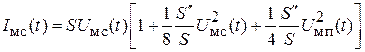(1.3)

Из полученного выражения следует, что амплитуда выходного сигнала зависит от амплитуды полезного сигнала и помехи, появляются нелинейные искажения в законе огибающей полезного сигнала, амплитудная модуляция помехи переносится на выход усилительного каскада в виде паразитной модуляции.

Если на вход УК воздействует смесь двух помех от соседних каналов, 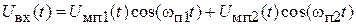, то возникает интермодуляционная помеха.

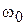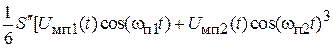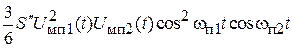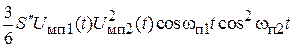Ее возникновение объясняется вкладом кубического слагаемого передаточной характеристики в образование тока на частоте . В выражении появляются два слагаемых и , которые образуют комбинационные частоты 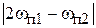и .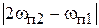

Если частоты 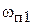и 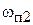удовлетворяют равенству 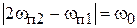или 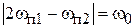, то образуется колебание 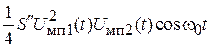или 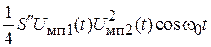, которое является интермодуляционной помехой.

Нелинейные искажения принято оценивать коэффициентами нелинейных искажений и коэффициентом гармоник. Рассмотрим сначала коэффициент нелинейных искажений. Пусть помеха соседнего канала отсутствует .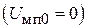

Тогда амплитуда тока на частоте 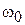равна 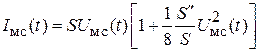. Зададим сообщение 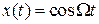низкочастотным гармоническим колебанием с частотой .

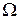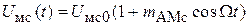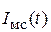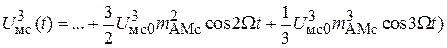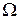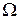При подстановке в после раскрытия скобок и возведения в степень в выражении появляются составляющие с частотами , 2 , 3 .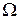

Коэффициент нелинейных искажений по k -ой гармонике представляет собой отношение амплитуды k -ой гармоники 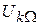к амплитуде первой гармоники 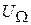. Амплитуда первой гармоники равна 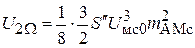, второй 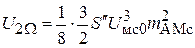и третьей .

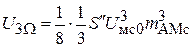Коэффициент нелинейных искажений по второй гармонике 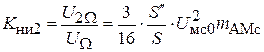и коэффициент нелинейных искажений по третьей гармонике 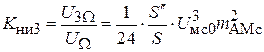. Коэффициент нелинейных искажений 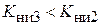. Поэтому, как правило, ограничиваются рассмотрением .

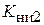По определению коэффициент гармоник .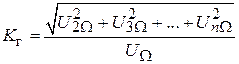

Коэффициент нелинейных искажений 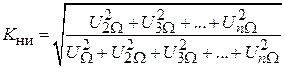выражается через коэффициент гармоник .

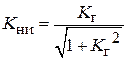Из полученных выражений следует, что снижение коэффициентов нелинейных искажений можно обеспечить:

1.Уменьшением отношения 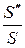. Это достигается выбором усилительного прибора с квадратической передаточной характеристикой, у которой 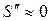. Такими характеристиками обладают полевые транзисторы и электронные лампы.

2. Контролем уровень сигнала 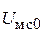с помощью системы АРУ.

3. Использованием при модуляции малых значений индекса амплитудной модуляции .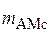

Для оценки перекрестных помех вводят понятие коэффициента перекрестных помех, под которым понимается отношение индекса модуляции перекрестной помехи на выходе к индексу модуляции помехи на входе.

Для нахождения этого коэффициента предположим, что модуляция полезного сигнала отсутствует, 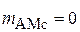, 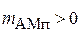. При подстановке в (1.3) 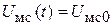и 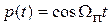выражение для амплитуды тока на частоте 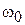приобретает вид:

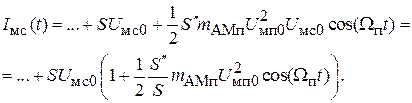
Выражение в скобках имеет вид огибающей АМ-помехи с индексом паразитной модуляции на выходе 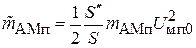. Коэффициент перекрестных помех 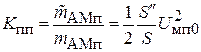. С его помощью можно найти отношение перекрестная помеха - сигнал на выходе УК:

.

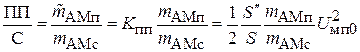Для уменьшения уровня перекрестных помех нужно выбирать УП с квадратической передаточной характеристикой, у которых 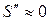и уменьшать амплитуду несущих колебаний помехи до основного усиления, т.е. использовать фильтры рассредоточенной избирательности.