| В матричной форме | По формулам Крамера | Методом Гаусса (метод последовательного исключения неизвестных) |
|
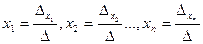 Важно!
Когда определитель системы
Важно!
Когда определитель системы  =0 и каждый определитель =0 и каждый определитель 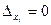 , то система имеет бесчисленное множество решений.
Когда определитель системы , то система имеет бесчисленное множество решений.
Когда определитель системы  =0 и хотя бы один из определителей =0 и хотя бы один из определителей 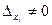 , система не имеет решений. , система не имеет решений.
| Метод состоит в следующем: систему уравнений приводят к эквивалентной ей системе в треугольной матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход). При выполнении прямого хода используют следующие преобразования: 1) умножение или деление коэффициентов свободных членов на одно и то же число; 2) сложение и вычитание уравнений; 3) перестановку уравнений системы; 4) исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю. |
Решение систем линейных уравнений
|
|

Сейчас читают про:
 2015-10-14
2015-10-14 360
360

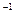 .
.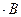 .
.





