2015-10-14
1748
Рассмотрим частные случаи плоских систем сил.
· Плоская система параллельных сил
В случае, когда все действующие на тело силы параллельны друг другу, можно для удобства направить ось Ox перпендикулярно силам. Тогда проекция каждой из сил на ось Ох будет равна нулю и первое из уравнений равновесия плоской системы сил обратится в тождество. В результате для плоской системы параллельных сил остаются два уравнения равновесия:
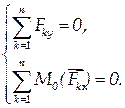| (1.33) |
· Плоская система сходящихся сил
В этом случае линии действия всех сил пересекаются в одной точке и их моменты относительно этой точки равны нулю, в силу чего моментное уравнение условий равновесия также обращается в тождество.
В результате получаем следующие уравнения равновесия:
| (1.34) |
В условиях равновесия для плоской системы сходящихся сил суммы проекций этих сил на координатные оси Ox и Oy равны нулю.
Теорема Вариньона об алгебраическом моменте равнодействующей силы.
Алгебраический момент равнодействующей плоской системы сил равен сумме алгебраических моментов сил системы.
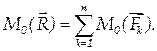| (1.35) |
Докажем это утверждение.
В соответствии с аксиомой статики 2, при добавлении к системе сил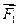 
, 
,..., 
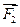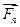с равнодействующей 
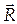уравновешивающей силы 
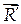тело будет находиться в равновесии. Уравнение моментов в условиях равновесия примет вид:
.
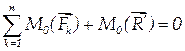Учитывая, что 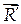= - 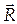, и обе силы имеют общую линию действия, то:
.
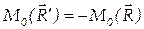Вычитая второе уравнение из первого, найдем:
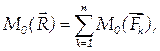
что и требовалось доказать.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Сформулируйте условия равновесия для плоской системы сил.
2. Чем отличаются условия равновесия для плоской системы параллельных сил от условий равновесия для плоской системы сходящихся сил?
3. Как найти момент равнодействующей в данной системе сил?
