Пусть дана система нелинейных уравнений специального вида:
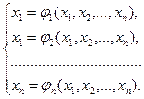
где функции 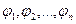 действительны и определены и непрерывны в некоторой окрестности
действительны и определены и непрерывны в некоторой окрестности 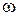 изолированного решения
изолированного решения 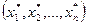 этой системы, или в более компактной записи:
этой системы, или в более компактной записи:
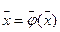 ,
,
где 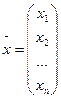 , а
, а 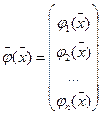 .
.
Для нахождения вектора-корня иногда можно использовать метод итерации
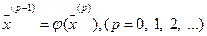 .
.
Если система уравнений задана в общем виде 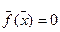 ,
,
где 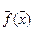 - вектор-функция, определенная и непрерывная в окрестности
- вектор-функция, определенная и непрерывная в окрестности 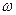 изолированного вектора-корня
изолированного вектора-корня 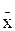 , то ее записывают в эквивалентном виде
, то ее записывают в эквивалентном виде
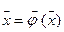 , (4.3)
, (4.3)
где 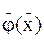 - итерирующая вектор-функция, которую ищут в виде
- итерирующая вектор-функция, которую ищут в виде
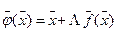 .
.
Матрица L выбирается так 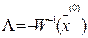 (см. выше). Предполагается, что матрица
(см. выше). Предполагается, что матрица 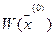 неособенная.
неособенная.
Подставив 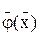 в (4.3), получим итерационную формулу
в (4.3), получим итерационную формулу
 .
.
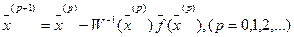
 2015-10-14
2015-10-14 477
477








