Пусть дана система двух уравнений с двумя неизвестными:
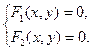
и требуется найти действительные корни системы с заданной степенью точности.
Предположим, что система допускает лишь изолированные корни. Число этих корней и их приближенные значения можно установить, построив кривые 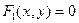 ,
, 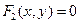 и определив координаты их точек пересечения.
и определив координаты их точек пересечения.
Для применения метода итераций система приводится к виду:
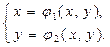
Функции 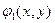 и
и 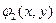 называются итерирующими. Алгоритм решения задается формулами
называются итерирующими. Алгоритм решения задается формулами
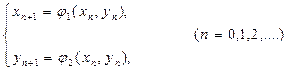 ,
,
где 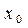 и
и 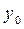 - некоторое начальное приближение.
- некоторое начальное приближение.
Имеет место следующая теорема.
Теорема 4.1 Пусть в некоторой замкнутой окрестности 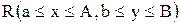 имеется одно и только одно решение
имеется одно и только одно решение 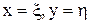 системы. Если:
системы. Если:
1. функции 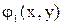 и
и 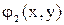 определены и непрерывно дифференцируемы в R,
определены и непрерывно дифференцируемы в R,
2. начальные приближения 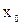 ,
, 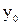 и все последующие приближения, xn,yn для n=1,2 … принадлежат R,
и все последующие приближения, xn,yn для n=1,2 … принадлежат R,
3. в R выполнены неравенства
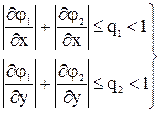 ,
,
то процесс последовательных приближений сходится к решению 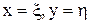 системы, т.е.
системы, т.е.
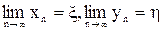 .
.
Эта теорема останется верной, если условие 3 заменить условием
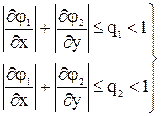
Оценка погрешности n -го приближения дается неравенством
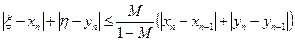 , (4.2)
, (4.2)
где M – наибольшее из чисел 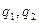 , входящих в неравенства. Сходимость метода итераций считается хорошей, если
, входящих в неравенства. Сходимость метода итераций считается хорошей, если 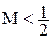 , при этом
, при этом 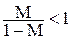 .
.
| Пример 4.3 Решить нелинейную систему уравнений методом итераций в Mathcad с точностью 0,005 Пусть дана система |
| Выразим из первого уравнения х, а из второго у и перепишем данную систему в виде: |
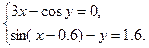
Отделение корней произведем графически. Построим функции 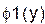 и
и 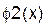 на одном графике. Они имеют одну точку пересечения в области
на одном графике. Они имеют одну точку пересечения в области
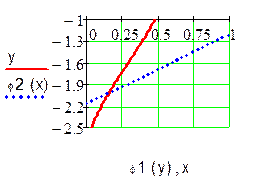
D(0 < x < 0.25; -1.9 < y < -2.2). Выберем за начальное приближение для метода итераций x0 = 0.25, y0 = -1.9
| Проверим условие сходимости теоремы в области D(а < x < b; c < y < d) |
| Считать будем до тех пор, пока не достигнем нужной точности |
| В данном случае метод итераций сходится достаточно медленно, так как значение М близко к единице Ответ: x=0.151 y=-2.034 |
Рис.4.3. Решение примера 4.3 в Mathcad
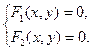
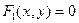 ,
, 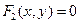 и определив координаты их точек пересечения.
и определив координаты их точек пересечения.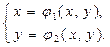
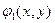 и
и 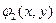 называются итерирующими. Алгоритм решения задается формулами
называются итерирующими. Алгоритм решения задается формулами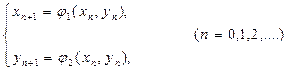 ,
,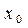 и
и 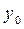 - некоторое начальное приближение.
- некоторое начальное приближение.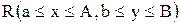 имеется одно и только одно решение
имеется одно и только одно решение 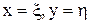 системы. Если:
системы. Если: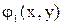 и
и 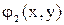 определены и непрерывно дифференцируемы в R,
определены и непрерывно дифференцируемы в R,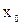 ,
, 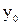 и все последующие приближения, xn,yn для n=1,2 … принадлежат R,
и все последующие приближения, xn,yn для n=1,2 … принадлежат R,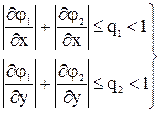 ,
,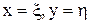 системы, т.е.
системы, т.е.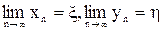 .
.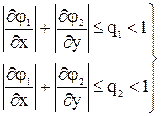
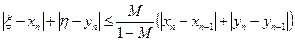 , (4.2)
, (4.2)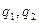 , входящих в неравенства. Сходимость метода итераций считается хорошей, если
, входящих в неравенства. Сходимость метода итераций считается хорошей, если 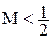 , при этом
, при этом 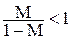 .
.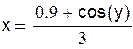
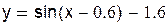
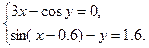
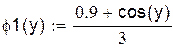
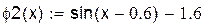
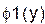 и
и 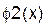 на одном графике. Они имеют одну точку пересечения в области
на одном графике. Они имеют одну точку пересечения в области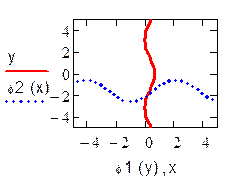
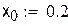
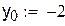
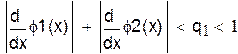
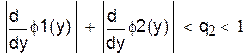
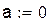
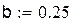
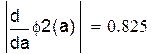
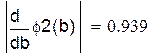
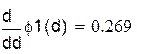
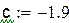
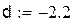
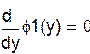
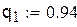
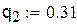
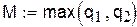
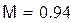
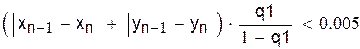
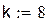
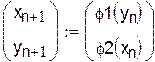

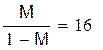
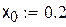

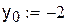

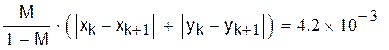
 2015-10-14
2015-10-14 980
980








