Скалярным произведением двух ненулевых векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними (рис.5.1), т.е.
называется число, равное произведению длин этих векторов на косинус угла между ними (рис.5.1), т.е.
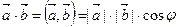 . (5.1)
. (5.1)
 |
Формула (5.1) можно записать в виде
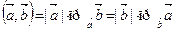 .
. Свойства скалярного произведения векторов
1. 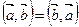 или
или 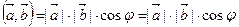 . (5.2)
. (5.2)
2. 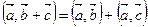 . (5.3)
. (5.3)
3. 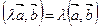 . (5.4)
. (5.4)
4. 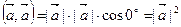 .
.
5. Если ненулевые векторы  и
и  взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е.
взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. 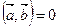 .
.
Векторы  и
и  , скалярное произведение которых равно нулю, называются ортогональными. Если заданы два вектора
, скалярное произведение которых равно нулю, называются ортогональными. Если заданы два вектора 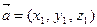 и
и 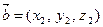 , то
, то
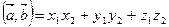 , (5.5)
, (5.5)
т.е. скалярное произведение двух векторов, заданных в координатной форме, равно сумме произведений одноименных координат.
Некоторые формулы, часто используемые при решении задач
1. Угол между двумя векторами.
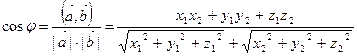 . (5.6)
. (5.6)
2. Необходимым и достаточным условием перпендикулярности двух векторов  и
и  является условие
является условие
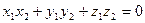 .
.
3. Условие параллельности (коллинеарности) двух векторов 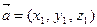 и
и 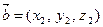 :
:
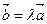 ,
, 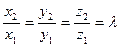 .
.
4. Проекция вектора на заданное направление.

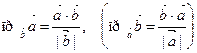 , т.е.
, т.е. 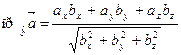 . (5.7)
. (5.7)
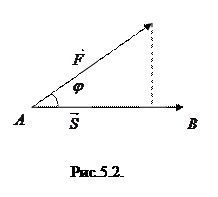 3. Работа постоянной силы.
3. Работа постоянной силы.
Пусть материальная точка перемещается прямолинейно из положения 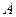 в положение
в положение 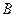 под действием силы
под действием силы 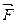 , образующей угол
, образующей угол 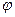 с перемещением
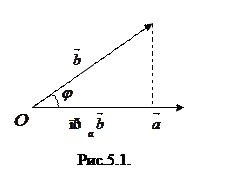
с перемещением 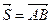 (рис.5.2). Известно, что работа силы
(рис.5.2). Известно, что работа силы 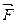 при перемещении
при перемещении 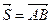 равна
равна
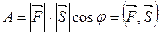 , (5.8)
, (5.8)
т.е. работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
Задача 5.1. Найти длину вектора 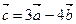 , если
, если 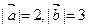 ,
, 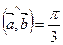 .
.
Решение. Имеем 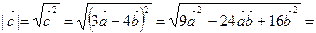
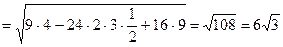 .
.
Задача 5.2. Доказать, что диагонали четырехугольника, вершины которого в точках 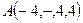 ,
, 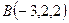 ,
, 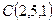 ,
, 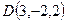 , взаимно перпендикулярны.
, взаимно перпендикулярны.
Решение. С помощью формулы (4.3) определим координаты векторов 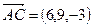 и
и 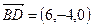 , лежащих на диагоналях четырехугольника и вычислим скалярное произведение
, лежащих на диагоналях четырехугольника и вычислим скалярное произведение 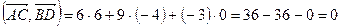 .
.
Так как выполнено условие перпендикулярности векторов, следовательно, 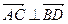 .
.
Задача 5.3. Вычислить работу, произведенную силой 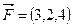 , если точка ее приложения перемещается прямолинейно из положения
, если точка ее приложения перемещается прямолинейно из положения 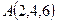 в положение
в положение 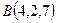 . Под каким углом к
. Под каким углом к 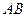 направлена сила
направлена сила 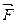 ?
?
Решение. По формуле (4.3) получим 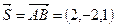 . Используя (5.8), находим
. Используя (5.8), находим 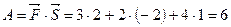 (ед.работы), угол
(ед.работы), угол 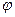 между
между 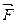 и
и 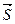 определим по формуле
определим по формуле 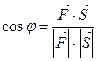 , т.е.
, т.е. 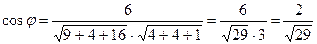 .
.
Отсюда, 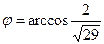 .
.
Задача 5.4. Выразить длину медианы произвольного треугольника через длины
его сторон.
Решение. Рассмотрим треугольник 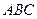 . Пусть
. Пусть 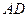 - одна из медиан треугольника (рис.5.3).
- одна из медиан треугольника (рис.5.3).
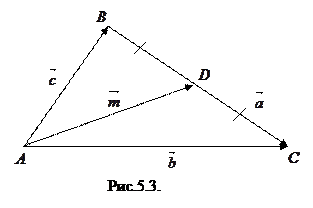 Введем в рассмотрение векторы
Введем в рассмотрение векторы 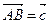 ,
, 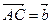 и
и 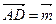 . Тогда
. Тогда 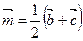 . Возведем обе части последнего равенства в квадрат:
. Возведем обе части последнего равенства в квадрат: 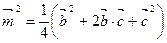 , отсюда получаем
, отсюда получаем
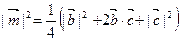 . (5.9).
. (5.9).
Из рисунка 5.3 имеем, что 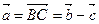 , отсюда
, отсюда 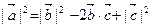 . Следовательно,
. Следовательно, 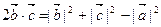 . Подставляя полученное выражение в правую часть равенства (5.9), находим
. Подставляя полученное выражение в правую часть равенства (5.9), находим 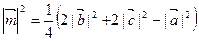 . Итак, длина медианы
. Итак, длина медианы 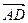 равна
равна 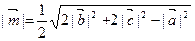 .
.
 2015-10-14
2015-10-14 2374
2374