Некоторые физические параметры (температура, масса, работа и др.) могут быть охарактеризованы одним числом, выражающим отношение рассматриваемой величины к другой однородной величине, принятой за единицу измерения. Такие величины называют скалярными; другие же величины (сила, скорость, ускорение) характеризуются числом и направлением и называются векторными. Для геометрического изображения физических векторных величин служат векторы.
Вектором называется направленный отрезок 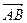 , в котором точка
, в котором точка 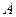 - начало, а точка
- начало, а точка 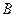 - конец. Векторы обозначаются символом
- конец. Векторы обозначаются символом 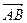 или
или  .
.
Модулем вектора называется длина вектора - скалярная величина, обозначаемая 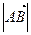 или
или 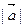 ,
, 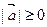 .Если
.Если 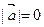 , то вектор
, то вектор  называется нулевым, если
называется нулевым, если 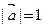 , то вектор
, то вектор  называется единичным вектором. Векторы
называется единичным вектором. Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Вектор, точка приложения которого может быть выбрана произвольно, называется свободным. Два вектора
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Вектор, точка приложения которого может быть выбрана произвольно, называется свободным. Два вектора  и
и  называются равными, если они имеют одинаковые длины, коллинеарны и сонаправлены.
называются равными, если они имеют одинаковые длины, коллинеарны и сонаправлены.
Проекцией вектора 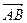 на ось
на ось 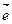 называется положительное число
называется положительное число 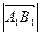 , если направление
, если направление 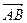 совпадает с направлением
совпадает с направлением 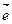 и отрицательное число
и отрицательное число 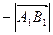 , если направление
, если направление 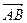 - противоположное направлению
- противоположное направлению 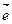 , где
, где 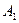 ,
, 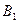 - проекции точек
- проекции точек 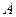 и
и  , соответственно, на указанную ось (рис. 4.1).
, соответственно, на указанную ось (рис. 4.1).
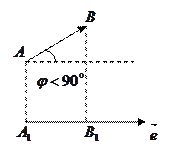  | 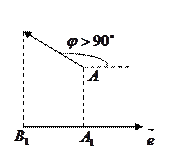 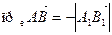 |
Рис.4.1.
Из определения проекции вектора вытекает, что 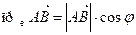 . Пусть вектор
. Пусть вектор 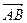 составляет угол
составляет угол 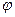 с осью
с осью 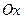 , тогда
, тогда
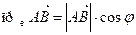 ,
, 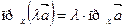 ,
, 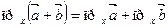 .
.
Под линейными операциями над векторами будем понимать операции сложения и вычитания векторов, а также умножение вектора на число.
Произведением вектора  на число (скаляр)
на число (скаляр) 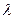 называется новый вектор, имеющий длину
называется новый вектор, имеющий длину 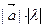 и сонаправленный с
и сонаправленный с  (при
(при 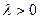 ) или противоположнонаправленный с
) или противоположнонаправленный с  (если
(если 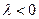 ). Геометрически, например, для
). Геометрически, например, для 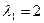 и
и 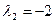 имеем векторы:
имеем векторы:

Суммой векторов  и
и  называется вектор
называется вектор 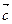 , замыкающий ломаную, построенную из данных векторов. Геометрически это выглядит следующим образом:
, замыкающий ломаную, построенную из данных векторов. Геометрически это выглядит следующим образом:
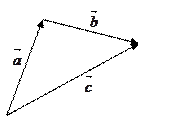 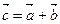 (правило треугольника); (правило треугольника); | 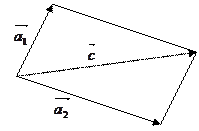 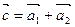 (правило параллелограмма); (правило параллелограмма); |
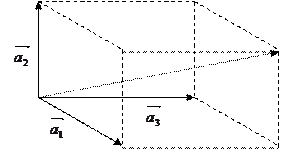 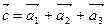 (правило параллелепипеда); (правило параллелепипеда); | 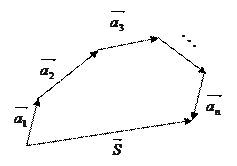 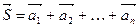 (правило замыкающей). (правило замыкающей). |
Линейные операции над векторами обладают следующими свойствами:
1. 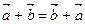 ,
,
2. 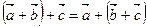 ,
,
3. 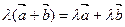 ,
,
4. 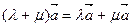 .
.
Прямоугольными декартовыми координатами точки 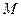 в пространстве называются числа
в пространстве называются числа 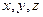 , выражающие величины векторов
, выражающие величины векторов 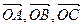 (рис.4.2), где
(рис.4.2), где 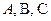 - проекции этой точки на взаимно перпендикулярные координатные оси: ось
- проекции этой точки на взаимно перпендикулярные координатные оси: ось 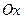 (ось абсцисс), ось
(ось абсцисс), ось 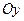 (ось ординат), ось
(ось ординат), ось 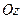 (ось аппликат).
(ось аппликат).
Радиусом-вектором точки 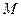 называется вектор
называется вектор 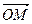 , начало которого совпадает с началом координат, а конец – с точкой
, начало которого совпадает с началом координат, а конец – с точкой 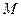 (рис.4.2).
(рис.4.2).
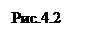 Векторы
Векторы 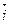 ,
, 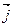 и
и 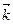 единичной длины,
единичной длины, 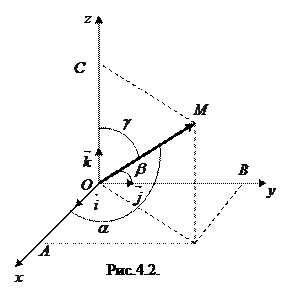 направления которых совпадают соответственно с направлениями осей координат
направления которых совпадают соответственно с направлениями осей координат 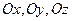 , называют ортами.
, называют ортами.
Направляющими косинусами вектора 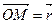 называются косинусы углов
называются косинусы углов 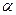 ,
, 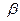 ,
, 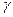 , образованных этим вектором с осями координат
, образованных этим вектором с осями координат 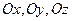 (
(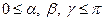 ).
).
Тогда 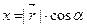 ,
, 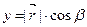 ,
, 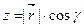 , (4.1) причем
, (4.1) причем 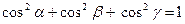 .
.
Если 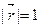 , то
, то 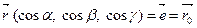 .
.
Теорема. Пусть 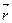 - вектор в пространстве
- вектор в пространстве 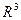 , а
, а 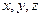 - его проекции на координатные оси, тогда вектор
- его проекции на координатные оси, тогда вектор 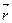 единственным образом можно представить в виде суммы произведений координат вектора
единственным образом можно представить в виде суммы произведений координат вектора 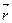 на соответствующие орты координатных осей.
на соответствующие орты координатных осей.
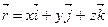 . (4.2)
. (4.2)
Векторное равенство (4.2) часто записывают в символической форме 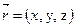 .
.
Некоторые формулы, используемые при решении задач:
1. Умножение вектора на число:
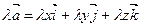 или
или 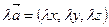 .
.
2. Сумма двух векторов:
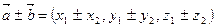 , где
, где 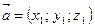 ,
, 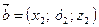 .
.
3. Расстояние между двумя точками.
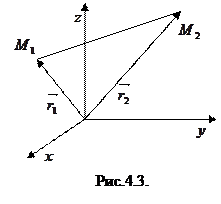 Если даны две точки:
Если даны две точки: 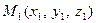 и
и 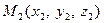 (рис.4.3),то координаты вектора
(рис.4.3),то координаты вектора 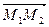 вычисляются по формуле:
вычисляются по формуле:
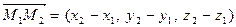 . (4.3)
. (4.3)
Расстояние между двумя точками определяется равенством:
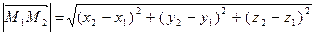 . (4.4)
. (4.4)
4. Деление отрезка в данном отношении.
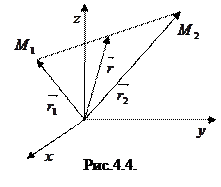 Пусть даны две точки
Пусть даны две точки 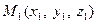 и
и 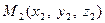 (рис.4.4), тогда координаты точки
(рис.4.4), тогда координаты точки 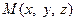 такой, что
такой, что 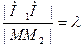 , определяются по формулам:
, определяются по формулам:
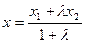 ,
, 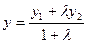 ,
, 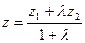 . (4.5)
. (4.5)
Если 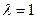 , то получим формулу для «деления отрезка пополам»:
, то получим формулу для «деления отрезка пополам»:
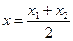 ,
, 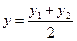 ,
, 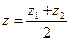 . (4.6)
. (4.6)
Задача 4.1. Даны две точки 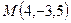 и
и 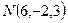 . Найти координаты вектора
. Найти координаты вектора 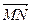 , его длину и определить направляющие косинусы.
, его длину и определить направляющие косинусы.
Решение. Используя формулу (4.3) получим: 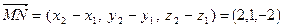 . По формуле (4.4) вычислим длину вектора
. По формуле (4.4) вычислим длину вектора 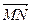 :
: 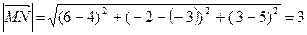 . Соотношения (4.1) позволяют определить направляющие косинусы вектора:
. Соотношения (4.1) позволяют определить направляющие косинусы вектора: 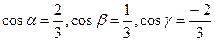 .
.
Задача 4.2. Даны векторы 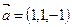 ,
, 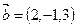 ,
, 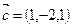 . Разложить вектор
. Разложить вектор 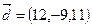 по векторам
по векторам 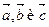 .
.
Решение. Пусть 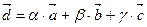 , где
, где 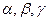 - некоторые неизвестные коэффициенты. Используя свойства линейных операций над векторами, получим систему уравнений:
- некоторые неизвестные коэффициенты. Используя свойства линейных операций над векторами, получим систему уравнений:
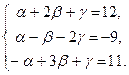
Решением последней системы уравнений будут значения 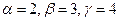 . Итак,
. Итак, 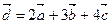 .
.
Задача 4.3. Для заданной силы 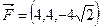 найти величину и направление.
найти величину и направление.
Решение. По формуле (4.4) находим величину силы 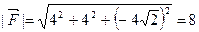 . Направляющие косинусы вектора
. Направляющие косинусы вектора 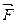 определяем с помощью равенств (4.1):
определяем с помощью равенств (4.1): 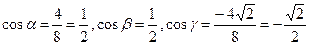 . Следовательно, сила с величиной
. Следовательно, сила с величиной 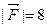 действует в направлении вектора, образующего с координатными осями углы
действует в направлении вектора, образующего с координатными осями углы 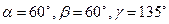 .
.
 2015-10-14
2015-10-14 1519
1519