Определение ускорений точек плоской фигуры

Ускорение каждой точки плоской фигуры (рис.25) равняется геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении плоской фигуры вокруг полюса:

. ()

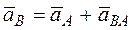Рисунок 25

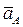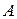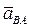Здесь – ускорение полюса , и – ускорение, которое имеет точка 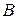при вращении плоской фигуры вокруг полюса .

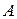При этом ускорение произвольной точки во вращательном движении имеет касательную и нормальную составляющие:

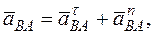
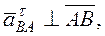
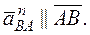
Модули этих составляющих

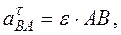
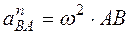. (133)

В общем случае полюс 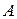может двигаться криволинейно и его ускорение 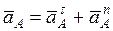, поэтому развернутая формула для определения ускорения произвольной точки плоской фигуры будет иметь четыре составляющих:

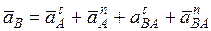. (134)

На рис.25 показано геометрическое определение вектора 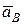построением соответствующего параллелограмма. На практике геометрическое сложение векторов при определении ускорения точки плоской фигуры удобнее осуществлять путем проектирования векторного выражения (134) на выбранные оси координат.