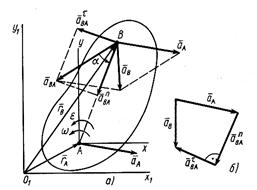
 Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом А и относительно вращательного вокруг А, по теореме о сложении ускорений для точки В имеем
Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом А и относительно вращательного вокруг А, по теореме о сложении ускорений для точки В имеем
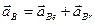 .
.
Так как переносное движение является поступательным вместе с точкой А фигуры, то переносное ускорение
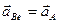 .
.
Относительное ускорение 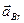 точки В от вращения вокруг полюса А обозначим
точки В от вращения вокруг полюса А обозначим 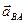 . После этого получается, что
. После этого получается, что

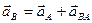 ,
,
т.е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
Ускорение от относительного вращательного движения вокруг полюса
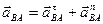 ,
,
причем
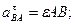
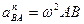
и
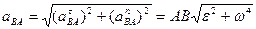 .
.
Касательное относительное ускорение 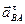 направлено по перпендикуляру к отрезку АВ в сторону дуговой стрелки углового ускорения
направлено по перпендикуляру к отрезку АВ в сторону дуговой стрелки углового ускорения 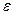 (рис.31,а).
(рис.31,а).
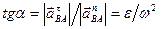 .
.
Угол 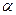 надо откладывать в направлении дуговой стрелки углового ускорения.
надо откладывать в направлении дуговой стрелки углового ускорения.
Формулу, определяющую зависимость ускорений двух точек плоской фигуры, можно получить непосредственным дифференцированием векторного равенства для скоростей, справедливого в любой момент времени. Имеем
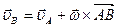 .
.
Продифференцируем по времени обе части этого равенства, учитывая изменения векторных величин относительно неподвижной системы координат (полные производные). Получаем
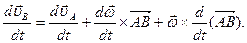
Здесь 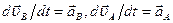 - ускорения точек В и А относительно неподвижной системы координат;
- ускорения точек В и А относительно неподвижной системы координат; 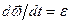 - угловое ускорение плоской фигуры.
- угловое ускорение плоской фигуры.
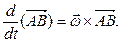
Объединяя полученные результаты, получаем
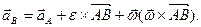
Рассуждения, аналогичные тем, которые проведены для скорости 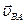 , позволяют сделать вывод о том, что
, позволяют сделать вывод о том, что
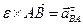 ;
; 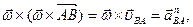
т.е. 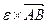 и
и 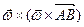 являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки А. Следовательно,
являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки А. Следовательно,
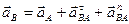 .
.
 2014-02-17
2014-02-17 2148
2148
