Теорема. Ускорение точки плоской фигуры равно сумме ускорения полюса 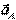 и ускорения данной точки во вращательном движении вокруг полюса
и ускорения данной точки во вращательном движении вокруг полюса 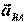
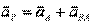 или
или 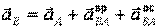 .
.
При плоском движении с учетом характера движения осестремительное ускорение называется центростремительным и обозначается символом 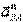 .
.
Следствие. Проекции ускорений двух точек плоской фигуры на направление вектора, соединяющего эти точки, связаны равенством
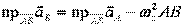 .
.
Другим следствием теоремы об ускорениях точек при плоском движении твердого тела является равенство:
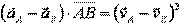 .
.
Вводя в рассмотрение вектор углового ускорения 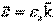 при плоском движении, теорема может быть записана в виде:
при плоском движении, теорема может быть записана в виде:
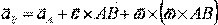 или
или 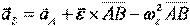 .
.
Проецируя на координатные оси, находим
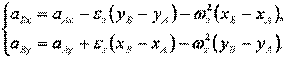 (2.4.2)
(2.4.2)
Эти уравнения могут быть использованы для определения неизвестных величин. При этом возможны два случая:
а) Если направление ускорения точки 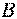 известно (или известны направления его составляющих), то из системы уравнений (2.4.2) находится ускорение этой точки, а также
известно (или известны направления его составляющих), то из системы уравнений (2.4.2) находится ускорение этой точки, а также 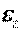 . При этом если знак
. При этом если знак 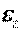 совпадает с
совпадает с 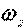 , то вращение плоской фигуры ускоренное.
, то вращение плоской фигуры ускоренное.
б) Если расстояние от какой-либо точки (например, точки A) плоской фигуры до мгновенного центра скоростей постоянно, то используется другой алгоритм решения. Сначала определяются скорость и ускорение точки A и эта точка принимается за полюс. Далее находится угловое ускорение по формуле
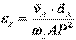 или
или 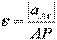 . (2.4.3)
. (2.4.3)
Затем из равенств (2.4.2) получаем проекции вектора ускорения произвольной точки 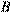 плоской фигуры на оси координат.
плоской фигуры на оси координат.
В учебной литературе доказывается, что при движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нолю. Эту точку называют мгновенным центром ускорений (МЦУ). В наших рассуждениях будем обозначать ее буквой Q. Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:
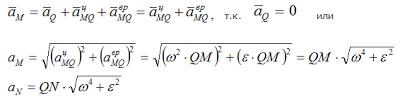
 2015-04-23
2015-04-23 6258
6258
