Тертя кочення

Між котком і площиною, на якій він знаходиться в стані спокою, виникають сили тертя, якщо прикласти до осі О котка силу 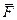, що намагається рухати його по площині. Розглянемо випадок, коли сила 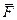паралельна до горизонтальної площини (рис. 6.1 а, б).

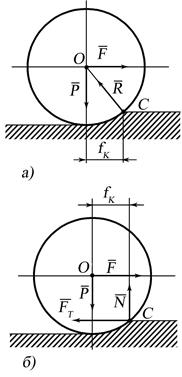З досвіду відомо, що при зміні величини сили від нуля до деякого граничного значення 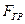коток залишається в спокої, тобто сили, які діють на коток, зрівноважені. Для зрівноваження заданих сил 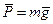і 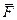до котка слід прикласти реакцію площини. З умови рівноваги трьох непаралельних сил випливає, що реакція 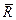площини повинна проходити через центр О котка, бо дві інші сили прикладені в цій точці. Це значить, що точка прикладання С реакції 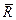повинна бути зміщена на відстань 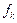від вертикалі, що проходить через центр колеса (рис. 6.1 а).

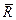Розкладемо реакцію на дві складові: нормальну складову 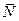і силу 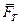, паралельну до площини (рис. 6.1 б).

У граничному положенні рівноваги котка до нього прикладені дві взаємно зрівноважені пари сил: одна пара (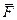, 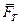), момент якої дорівнює 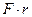(r - радіус котка), та друга пара сил 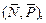момент якої дорівнює 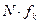, тобто:

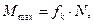(6.1)

де 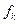- коефіцієнт тертя кочення. Цей коефіцієнт можна розглядати як відстань, на яку реакція 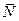зміщується від вертикалі, що проходить через центр котка.

Для того щоб коток котився, а не ковзав, треба щоб виконувалась умова:

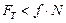, (6.2)

де 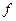- коефіцієнт тертя ковзання.

При розв'язуванні задач на рівновагу твердого тіла при наявності тертя кочення треба дотримуватись такої послідовності:

1) виділити тверде тіло, рівновагу якого треба дослідити;

2) вибрати систему координат;

3) показати задані сили;

4) застосувати принцип звільнення від в'язей і замінити в'язі їх реакціями;

5) скласти рівняння рівноваги для твердого тіла;

6) розв'язати одержану систему рівнянь.

Вказівка. Для закріплення теоретичного матеріалу §§ 5 - 6 необхідно розв’язати наступні задачі із збірника: Мещерский И.В. Сборник задач по теоретической механике. - М.: Наука, 1981 (або 1986):

1) №№ 5.1; 5.5; 5.8; 5.38;

2) №№ 5.11; 5.12; 5.15; 5.39; 5,40;

3) №№ 5.28; 5.31; 5.33; 5.42.