Рассмотрим составное высказывание, которое образуется из элементарных высказываний с помощью союза «и».
Союз «и» в русском языке имеет различные смысловые оттенки. Например, предложение «Кубик маленький и красный» будет истинным, если истинны оба составляющих предложения. А предложение «На этих местах сидят дети и инвалиды» истинно, если истинно хотя бы одно из составляющих предложений. В математической речи союз «и» употребляется только в первом смысле.
Пусть даны высказывания А и В.
Конъюнкцией высказываний А и В называется высказывание, которое истинно, когда истинны оба данные высказывания одновременно.
Конъюнкция высказываний А и В обозначается: АÙВ. Читаем: «Конъюнкция высказываний А и В» или «А и В».
Название «конъюнкция» произошло от латинского слова «conjunctio», что означает «союз, связь или единение». Определение конъюнкции высказываний А и В можно записать в следующей таблице.
| А | В | АÙВ |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Замечание. В этой таблице, кроме первой строки для обозначения высказываний, еще – 4 строки для комбинаций значений истинности высказываний А и В. Для подсчета числа комбинаций используется комбинаторная задача – размещение с повторениями, т.к. мы два значения истинности («и» или «л») распределяем на два высказывания.
Используя формулу для подсчета числа размещений с повторениями Ā  =m
=m 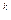 , получаем Ā
, получаем Ā 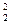 = 2² = 4. Если данных высказываний будет 3, то комбинаций (строк) будет 8 по той же формуле Ā
= 2² = 4. Если данных высказываний будет 3, то комбинаций (строк) будет 8 по той же формуле Ā 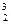 = 2³ = 8. Для четырех данных высказываний число комбинаций значений истинности и, соответственно, число строк будет равно уже 16, т.к. Ā
= 2³ = 8. Для четырех данных высказываний число комбинаций значений истинности и, соответственно, число строк будет равно уже 16, т.к. Ā 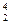 = 2
= 2 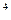 = 16.
= 16.
Примеры.
1. Составное высказывание «Число 2 чётное и простое» будет истинным, т.к. оно является конъюнкцией двух истинных высказываний «Число 2 чётное» и «Число 2 простое».
2. Составное высказывание «Число 14 четное и простое» будет ложным, т.к. оно представляет собой конъюнкцию двух высказываний «Число 14 четное» и «Число 14 простое», из которых первое истинно, а второе ложно.
3. Составное высказывание «8<5<4» будет также ложным, т.к. является конъюнкцией двух ложных высказываний «8<5» и «5<4».




 4. Пример использования составного высказывания «А и В» в работе с дошкольниками. Наглядный материал изображён на рисунке 16:
4. Пример использования составного высказывания «А и В» в работе с дошкольниками. Наглядный материал изображён на рисунке 16:
 Задание ребенку: «Возьми
Задание ребенку: «Возьми
чёрный треугольник». Рис. 16
Элементарные предложения: А – «фигура треугольной формы», В – «фигура чёрного цвета».
| Выбор ребёнка | Значение истинности элементарных предложений | Оценка воспитателя | |
| А | В | ||
 | и | и | «правильно» |
 | и | л | «неправильно» |
 | л | и | «неправильно» |
 | л | л | «неправильно» |
Замечание. В обыденной речи конъюнкция может выражаться не только с помощью союза «и», но и другими, например, «а», «но», «однако», «не только…, но и …».
Например, «Число 16 делится не только на 2, но и на 4».
Рассмотрим составное высказывание, которое образуется из элементарных высказываний с помощью союза «или».
Предложение «Идет дождь или светит солнце» будет истинным, если истинно хотя бы одно из составляющих предложений, причем не исключается возможность истинности обоих предложений. Именно в этом смысле понимается союз «или» и в математическом языке.
Пусть даны высказывания А и В.
Дизъюнкцией высказываний А и В называется высказывание, которое истинно, когда истинно хотя бы одно из данных высказываний.
Дизъюнкция высказываний А и В обозначается: А  В. Читаем: «Дизъюнкция высказываний А и В» или «А или В».
В. Читаем: «Дизъюнкция высказываний А и В» или «А или В».
Название «дизъюнкция» произошло от латинского слова «disjunctio», что означает «разделение, разобщение».
Определение дизъюнкции высказываний А и В можно записать в следующей таблице.
| А | В | А  В В |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Примеры.
1. Составное высказывание «Число 14 чётное или простое» будет истинным, т.к. оно представляет собой дизъюнкцию высказываний «Число 14 чётное» и «Число 14 простое», где первое – истинно, а второе – ложно.
2. Составное высказывание «Число 36 делится на 6 или на 9» будет также истинным, т.к. оно является дизъюнкцией двух истинных высказываний «Число 36 делится на 6» и «Число 36 делится на 9».
3. Составное высказывание «4≥6» будет ложным, т.к. оно представляет собой дизъюнкцию двух ложных высказываний «4>6» и «4=6».
4. Пример использования составного высказывания «А или В» в работе с детьми дошкольного возраста. Наглядный материал изображён на рисунке 17:
Задание ребенку: «Возьми фигуру, похожую на яблоко по цвету или по форме».







Рис. 17
Элементарные предложения: А – «форма как у яблока», В – «цвет как у яблока».
| Выбор ребенка | Значение истинности элементарных предложений | Оценка воспитателя | |
| А | В | ||
 | и | и | «правильно» |
 | и | л | «правильно» |
 | л | и | «правильно» |
 | л | л | «неправильно» |
Замечание. Определения конъюнкции и дизъюнкции двух высказываний можно обобщить на n составляющих их высказываний.
Конъюнкцией высказываний A 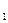 , А
, А 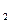 , …, А
, …, А  называется высказывание, которое истинно, когда истинны все данные высказывания одновременно.
называется высказывание, которое истинно, когда истинны все данные высказывания одновременно.
Дизъюнкцией высказываний A 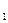 , А
, А  , …, А
, …, А  называется высказывание, которое истинно, когда истинно хотя бы одно из данных высказываний.
называется высказывание, которое истинно, когда истинно хотя бы одно из данных высказываний.
Для операций конъюнкции и дизъюнкции высказываний выполняются одинаковые законы, поэтому рациональнее рассматривать их одновременно.
I. Закон коммутативности
а) конъюнкции высказываний: (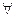 A,B)(A
A,B)(A  B=B
B=B  A),
A),
б) дизъюнкции высказываний: (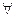 A,B)(A
A,B)(A  B=B
B=B  A).
A).
I а) читаем: «Для любых высказываний А и В конъюнкция высказываний А и В равносильна конъюнкции высказываний В и А».
I б) читаем: «Для любых высказываний А и В дизъюнкция высказываний А и В равносильна дизъюнкции высказываний В и А».
Название этого закона произошло от латинского слова «commutatio», что означает «перемена», поэтому закон иначе называется переместительным (от перемены мест высказываний конъюнкция или дизъюнкция не меняется).
Доказательство законов Iа и Iб проводят в таблицах истинности.
Iа Iб
| А | В | A B B | B A A | А | В | A B B | B A A | |
| и | и | и | и | и | и | и | и | |
| и | л | л | л | и | л | и | и | |
| л | и | л | л | л | и | и | и | |
| л | л | л | л | л | л | л | л |
Сравнивая в этих таблицах значения истинности для результатов операций A  B и B
B и B  A (A
A (A  B и B
B и B  A) по строкам, убеждаемся, что эти значения совпадают, следовательно, составные высказывания A
A) по строкам, убеждаемся, что эти значения совпадают, следовательно, составные высказывания A  B и B
B и B  A (A
A (A  B и B
B и B  A) равносильны, а равенства: A
A) равносильны, а равенства: A  B = B
B = B  A и A
A и A  B = B
B = B  A верны.
A верны.
II. Закон ассоциативности
а) конъюнкции высказываний: (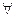 A,B,C)[A
A,B,C)[A  (B
(B  C)=(A
C)=(A  B)
B)  C],
C],
б) дизъюнкции высказываний: (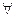 A,B,C)[A
A,B,C)[A  (B
(B  C)=(A
C)=(A  B)
B)  C].
C].
II а) читаем: «Для любых высказываний А, В и С конъюнкция высказывания А с конъюнкцией высказываний В и С равносильна конъюнкции высказывания С с конъюнкцией высказываний А и В».
II б) читаем: «Для любых высказываний А, В и С дизъюнкция высказывания А с дизъюнкцией высказываний В и С равносильна дизъюнкции высказывания С с дизъюнкцией высказываний А и В».
Название закона произошло от латинского слова «associatio», что означает «сочетание, соединение», поэтому он иначе называется сочетательным (от перемены мест скобок конъюнкция или дизъюнкция не меняется).
В следующей таблице истинности докажем закон II а.
| А | В | С | B C C | A (B (B C) C) | A B B | (A B) B) C C |
| и | и | и | и | и | и | и |
| и | и | л | л | л | и | л |
| и | л | и | л | л | л | л |
| и | л | л | л | л | л | л |
| л | и | и | и | л | л | л |
| л | л | и | л | л | л | л |
| л | л | л | л | л | л | л |
* *
Сравнивая в этой таблице по строкам значения истинности для результатов операций A  (B
(B  C) и (A
C) и (A  B)
B)  C (столбцы, помеченные знаком «*»), убеждаемся, что эти значения совпадают, следовательно, равенство A
C (столбцы, помеченные знаком «*»), убеждаемся, что эти значения совпадают, следовательно, равенство A  (B
(B  C)=(A
C)=(A  B)
B)  C – верно.
C – верно.
Закон II б предлагается доказать самостоятельно.
а) конъюнкции относительно дизъюнкции: (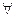 A,B,C)[A
A,B,C)[A  (B
(B  C)= (A
C)= (A  B)
B)  (А
(А  C)],
C)],
б) дизъюнкции относительно конъюнкции: (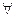 A,B,C)[A
A,B,C)[A  (B
(B  C)= (A
C)= (A  В)
В)  (A
(A  C)].
C)].
Название закона произошло от латинского слова «distributio», что означает «распределение», поэтому иначе его называют распределительным законом.
III а) читаем: «Для любых высказываний А, В и С конъюнкция высказывания А с дизъюнкцией высказываний В и С равносильна дизъюнкции конъюнкции А и В с конъюнкцией высказываний А и С».
III б) читаем: «Для любых высказываний А, В и С дизъюнкция высказывания А с конъюнкцией высказываний В и С равносильна конъюнкции дизъюнкции А и В с дизъюнкцией А и С».
Докажем закон IIIа дистрибутивности конъюнкции относительно дизъюнкции, используя таблицу истинности и определения операций конъюнкции и дизъюнкции.
| А | В | С | B C C | A (B (B C) C) | A B B | A С С | (A B) B) (А (А C) C) |
| и | и | и | и | и | и | и | и |
| и | и | л | и | и | и | л | и |
| и | л | и | и | и | л | и | и |
| и | л | л | л | л | л | л | л |
| л | и | и | и | л | л | л | л |
| л | и | л | и | л | л | л | л |
| л | л | и | и | л | л | л | л |
| л | л | л | л | л | л | л | л |
* *
Сравнивая по строкам значения истинности для результатов операций A  (B
(B  C) и (A
C) и (A  B)
B)  (А
(А  C) (столбцы, помеченные знаком «*»), убеждается, что все значения совпадают, значит составные высказывания A
C) (столбцы, помеченные знаком «*»), убеждается, что все значения совпадают, значит составные высказывания A  (B
(B  C) и (A
C) и (A  B)
B)  (А
(А  C) равносильны и равенство A
C) равносильны и равенство A  (B
(B  C) = (A
C) = (A  B)
B)  (А
(А  C) – верно.
C) – верно.
Закон III б предлагается доказать самостоятельно.
IV. Законы де Моргана
а) отрицание конъюнкции: (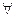 A,B) (
A,B) ( =`А
=`А  `B),
`B),
б) отрицание дизъюнкции: (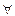 A,B)(
A,B)(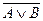 =`А
=`А  `B).
`B).
Законы названы именем шотландского математика де Моргана (1806 -1871 гг.).
IV а) читаем: «Для любых высказываний А и В отрицание конъюнкции высказываний А и В равносильно дизъюнкции отрицаний высказываний А и В».
IV б) читаем: «Для любых высказываний А и В отрицание дизъюнкции высказываний А и В равносильно конъюнкции отрицаний высказываний А и В».
Доказательство этих законов выполнено в следующих таблицах.
IV а IV б
| А | В | A B B |  | Ā | `В | `А `B `B | А | В | A B B | 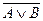 | Ā | `В | `А  `B `B | |
| и | и | и | л | л | л | л | и | и | и | л | л | л | л | |
| и | л | л | и | л | и | и | и | л | и | л | л | и | л | |
| л | и | л | и | и | л | и | л | и | и | л | и | л | л | |
| л | л | л | и | и | и | и | л | л | л | и | и | и | и |
* * * *
Сравнивая по строкам значения истинности для результатов операций  и `А
и `А  ` B в левой таблице (
` B в левой таблице (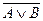 и `А
и `А  ` B – в правой таблице) в столбцах, отмеченным знаком «*», убеждаемся, что все значения совпадают, значит, законы де Моргана доказаны.
` B – в правой таблице) в столбцах, отмеченным знаком «*», убеждаемся, что все значения совпадают, значит, законы де Моргана доказаны.
Рассмотрим применение этих законов на следующих примерах.
1. Даны высказывания А: «5>3» и В: «4=5», где А – и, а В – л. Образуем конъюнкцию данных высказываний: A  B: «5>3 и 4=5» - она ложна. Ее отрицание:
B: «5>3 и 4=5» - она ложна. Ее отрицание:  : «Неверно, что 5>3 и 4=5». Чтобы определить значение истинности этого составного высказывания, воспользуемся законом де Моргана
: «Неверно, что 5>3 и 4=5». Чтобы определить значение истинности этого составного высказывания, воспользуемся законом де Моргана  = `А
= `А 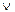 ` B. Тогда имеем `А
` B. Тогда имеем `А  ` B: «5`>3 или 4≠5» или «5≤3 или 4≠5», это составное высказывание истинно, т.к. «5≤3» - л, а «4≠5» - и.
` B: «5`>3 или 4≠5» или «5≤3 или 4≠5», это составное высказывание истинно, т.к. «5≤3» - л, а «4≠5» - и.
2. Из высказываний А: «6M2» и В: «4<8», из которых оба истинны, образуем дизъюнкцию A 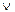 B: «6M2 или 4<8» (она «и»), а теперь – её отрицание
B: «6M2 или 4<8» (она «и»), а теперь – её отрицание 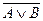 : «Неверно, что 6M2 или 4<8». Используя закон де Моргана
: «Неверно, что 6M2 или 4<8». Используя закон де Моргана 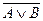 = `А
= `А  ` B, получим A
` B, получим A 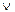 B = `А
B = `А  ` B: «6`M2 и 4`<8» или «6 не кратно 2 и 4≥8»; это составное высказывание ложно, т.к. оба составляющие высказывания «6 не кратно 2» и «4≥8» ложны.
` B: «6`M2 и 4`<8» или «6 не кратно 2 и 4≥8»; это составное высказывание ложно, т.к. оба составляющие высказывания «6 не кратно 2» и «4≥8» ложны.
V. а) Закон противоречия: ( A) (A
A) (A  Ā=л).
Ā=л).
б) Закон исключения третьего: (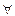 A)(A
A)(A 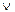 Ā=и).
Ā=и).
V а) читаем: «Для любого высказывания А конъюнкция высказывания А с его отрицанием есть ложное высказывание».
V б) читаем: «Для любого высказывания А дизъюнкция высказывания А с его отрицанием есть истинное высказывание».
Доказательство законов V а и V б приведено в следующих таблицах.
V а V б
| А | Ā | A Ā Ā | А | Ā | A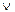 Ā Ā | |
| и | л | л | и | л | и | |
| л | и | л | л | и | и |
В левой таблице значения истинности для составного высказывания A  Ā все ложны, а это и значит, что A
Ā все ложны, а это и значит, что A  Ā=л. В правой таблице значения истинности для высказывания A
Ā=л. В правой таблице значения истинности для высказывания A 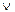 Ā все истинны, т.е. A
Ā все истинны, т.е. A 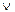 Ā=и.
Ā=и.
Замечание. В логике считается, что операция конъюнкции «сильнее» операции дизъюнкции, поэтому, если в составном высказывании есть знаки операций конъюнкции и дизъюнкции и нет скобок, то сначала выполняют конъюнкцию, а затем дизъюнкцию.
Например, порядок выполнения действий в составном высказывании A 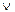 В
В  C будет такой: сначала находят конъюнкцию высказываний В и С, а затем – дизъюнкцию высказывания А с полученным составным высказыванием В
C будет такой: сначала находят конъюнкцию высказываний В и С, а затем – дизъюнкцию высказывания А с полученным составным высказыванием В  С.
С.
Согласно этому замечанию, например, закон дистрибутивности конъюнкции относительно дизъюнкции (см. III а) можно записать: ( A,B,C)[A
A,B,C)[A  ( B
( B 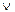 C)=A
C)=A  B
B  A
A  C].
C].
 2015-10-22
2015-10-22 15603
15603
