Логические операции. Дизъюнкция, конъюнкция и отрицание

Логические основы ЭВМ

Алгебра логики и логические основы компьютера

Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.

Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.

Логические операции. Дизъюнкция, конъюнкция и отрицание

Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6».

Как мы решаем, что нам сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае правдивости обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным.

Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.

Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, т.к. с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем. Такими операциями являются конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ). Часто конъюнкцию обозначают &, дизъюнкцию - ||, а отрицание - чертой над переменной, обозначающей высказывание.

При конъюнкции@/a> истина с ложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.

При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.

Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.

Для логических величин обычно используются три операции:

Конъюнкция – логическое умножение (И) – and, &, ∧.

Дизъюнкция – логическое сложение (ИЛИ) – or, |, v.

Логическое отрицание (НЕ) – not,.

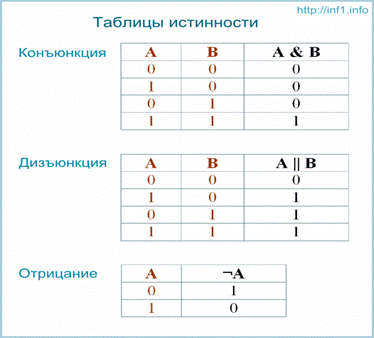
Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).

Логические основы компьютера

В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.

Переключательные схемы

В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.

Вентили, триггеры и сумматоры

Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.

Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.

Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.

Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.

Информация и информационные процессы. Виды информации, её двоичное кодирование. Количество информации, подходы к определению понятия «количество информации», единицы измерения информации. Двоичное кодирование числовой, текстовой, графической, звуковой информации

Информация (от лат. informatio — «разъяснение, изложение, осведомлённость») — сведения о чём-либо, независимо от формы их представления.

В настоящее время не существует единого определения информации как научного термина. С точки зрения различных областей знания данное понятие описывается своим специфическим набором признаков. Понятие «информация» является базовым в курсе информатики, где невозможно дать его определение через другие, более «простые» понятия.

Свойства информации:

- Объективность (информация объективна, если она не зависит от чьего-либо мнения, суждения);

- Достоверность (информация достоверна, если она отражает истинное положение дел);

- Полнота (информация полна, если ее достаточно для понимания и принятия решения);

- Актуальность (информация актуальна, своевременна, если она важна, существенна для настоящего времени);

- Полезность (оценивается по тем задачам, которые мы можем решить с ее помощью);

- Понятность (информация понятна, если она выражена на языке, доступном для получателя);

- Доступность (информация доступна, если мы можем её получить).

Информационный процесс - совокупность последовательных действий (операций), производимых над информацией (в виде данных, сведений, фактов, идей, гипотез, теорий и пр.), для получения какого-либо результата (достижения цели).

Информация проявляется именно в информационных процессах. Информационные процессы всегда протекают в каких-либо системах (социальных, социотехнических, биологических и пр.).

Наиболее обобщенными информационными процессами являются сбор, преобразование, использование информации.

К основным информационным процессам, изучаемым в курсе информатики, относятся: поиск, отбор, хранение, передача, кодирование, обработка, защита информации.

Информационные процессы, осуществляемые по определенным информационным технологиям, составляет основу информационной деятельности человека.

Компьютер является универсальным устройством для автоматизированного выполнения информационных процессов.

Люди имеют дело со многими видами информации. Общение людей друг с другом дома и в школе, на работе и на улице – это передача информации. Учительский рассказ или рассказ товарища, телевизионная передача, телеграмма, письмо, устное сообщение и т.д. – все это примеры передачи информации.

И мы уже говорили о том, что одну и ту же информацию можно передать и получить различными путями. Так, чтобы найти дорогу в музей в незнакомом городе, можно спросить прохожего, получить справку в справочном бюро, попытаться разобраться самому с помощью плана города или обратиться к путеводителю. Когда мы слушаем объяснение учителя, читаем книги или газеты, смотрим новости ТВ, посещаем музеи и выставки – в это время мы получаем информацию.

Человек хранит полученную информацию в голове. Мозг человека – огромное хранилище информации. Блокнот или записная книжка, ваш дневник, школьные тетрадки, библиотека, музей, кассета с записями любимых мелодий, видеокассеты – все это примеры хранения информации.

Информацию можно обрабатывать: перевод текста с английского языка на русский и наоборот, вычисление суммы по заданным слагаемым, решение задачи, раскрашивание картинок или контурных карт – все это примеры обработки информации. Все вы любили в свое время раскрашивать книжки-раскраски. Оказывается, в это время вы занимались важным процессом – обработкой информации, черно-белый рисунок превращали в цветной.

Информацию можно даже терять. Допустим, Иванов Дима забыл дневник дома и поэтому записал домашнее задание на листочке. Но, играя на перемене, он сделал из него самолетик и запустил его. Придя домой, Дима не смог сделать домашнюю работу, он потерял информацию. Теперь ему нужно или попытаться вспомнить, что же ему задали, или позвонить однокласснику, чтобы получить нужную информацию, или идти в школу с невыполненным домашним заданием.

Двоичное кодирование – один из распространенных способов представления информации. В вычислительных машинах, в роботах и станках с числовым программным управлением, как правило, вся информация, с которой имеет дело устройство, кодируется в виде слов двоичного алфавита.

Двоичный алфавит состоит из двух цифр 0 и 1.

Цифровые ЭВМ (персональные компьютеры относятся к классу цифровых) используют двоичное кодирование любой информации. В основном это объясняется тем, что построить техническое устройство, безошибочно различающее 2 разных состояния сигнала, технически оказалось проще, чем то, которое бы безошибочно различало 5 или 10 различных состояний.

К недостаткам двоичного кодирования относят очень длинные записи двоичных кодов, что затрудняет работу с ними.