Определение 1. Высказыванием называется любое верифицируемое повествовательное предложение, т.е. предложение, относительно которого можно утверждать истинно оно или ложно.
Пример «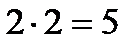 » – высказывание; «сегодня хорошая погода» – не высказывание (для кого как!).
» – высказывание; «сегодня хорошая погода» – не высказывание (для кого как!).
Определение 2. Предложение, содержащее переменную и обращающееся в высказывание при подстановке конкретных значений называют высказывательной формой.
Пример. 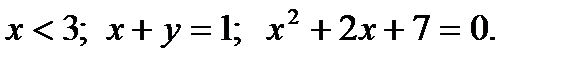
Определение 3. Множество всех возможных истинных интерпретаций высказывания называется смысловым полем (интерпретация – это форма представления информации).
Смысловое поле задано на своём универсуме – множестве всех возможных интерпретаций. Это позволяет высказывания, как и множества, изображать кругами Эйлера. В этом случае характеристическая функция для высказываний имеет вид:

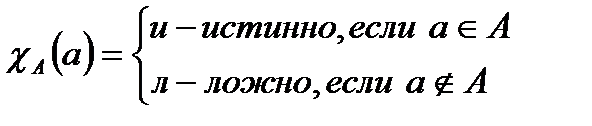 .
.
A – высказывание, а – его интерпретация.
Определение 4. Сложным называется высказывание, составленное из простых с помощью логических операций: ù – неверно, что;  – конъюнкция;
– конъюнкция;  – дизъюнкция;
– дизъюнкция; 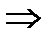 – импликация;
– импликация; 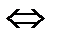 – эквивалентность; и кванторов:
– эквивалентность; и кванторов: 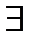 – существует,
– существует,  – для всех,
– для всех, 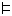 - тавтология (всегда истинно).
- тавтология (всегда истинно).
Опишем эти операции, используя понятие смыслового поля:

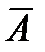 или ù А – неверно, что А;
или ù А – неверно, что А;

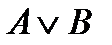 –дизъюнкция («или»), совокупность (disjunctio – различие);
–дизъюнкция («или»), совокупность (disjunctio – различие);

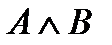 –конъюнкция («и»), система (conjunctio – союз);
–конъюнкция («и»), система (conjunctio – союз);

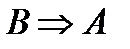 –импликация, теорема (implictio – тесно связывать);
–импликация, теорема (implictio – тесно связывать);

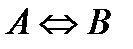 – эквивалентность (или
– эквивалентность (или 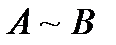 ).
).
Это описание позволяет составить таблицы истинности для этих операций.
| A | B | 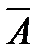
| 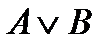
| 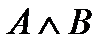
| 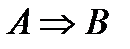
| 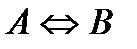
|
| и | и | л | и | и | и | и |
| и | л | л | и | л | л | л |
| л | и | и | и | л | и | л |
| л | л | и | л | л | и | и |
Теперь можно точно дать определения.
Определение 5 Дизъюнкцией двух высказываний 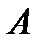 и
и 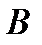 называется новое сложное высказывание
называется новое сложное высказывание 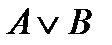 , которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний
, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний 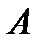 или
или 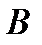 .
.
Определение 6. Конъюнкцией двух высказываний … (самостоятельно)
Определение 7. Эквиваленцией … (самостоятельно).
Определение 8. Импликацией двух высказываний 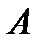 и
и 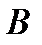 называется новое сложное высказывание
называется новое сложное высказывание 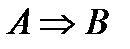 , которое ложно тогда и только тогда, когда высказывание
, которое ложно тогда и только тогда, когда высказывание 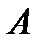 истинно, а высказывание
истинно, а высказывание 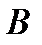 ложно.
ложно.
Импликация 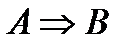 называется ещё теоремой. Тогда говорят, что
называется ещё теоремой. Тогда говорят, что 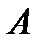 достаточное условие для
достаточное условие для 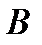 ,
, 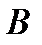 – необходимое условие для
– необходимое условие для 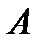 . Теорема
. Теорема 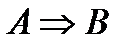 называется прямой,
называется прямой, 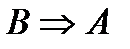 – обратной,
– обратной, 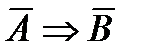 – противоположная прямой,
– противоположная прямой, 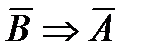 – противоположная обратной. Используя таблицы истинности, докажем три важных факта:
– противоположная обратной. Используя таблицы истинности, докажем три важных факта:
Теорема 1. Теорема 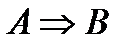 эквивалентна теореме
эквивалентна теореме 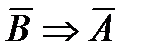 .
.
Теорема 2. Теорема 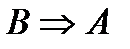 эквивалентна
эквивалентна 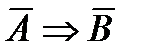 .
.
Теорема 3. Теорема 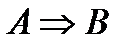 эквивалентна дизъюнкции
эквивалентна дизъюнкции 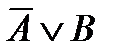 .
.

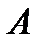
| 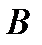
| 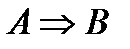
| 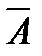
| 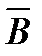
| 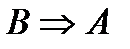
| 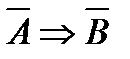
| 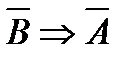
| 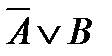
|
| и | и | и | л | л | и | и | и | и |
| и | л | л | л | и | и | и | л | л |
| л | и | и | и | л | л | л | и | и |
| л | л | и | и | и | и | и | и | и |
■
Теоремы 1 и 2 называют законом контрапозиции, а теорему 3 – дизъюнктивной формой импликации.
 2015-03-22
2015-03-22 454
454








