2015-10-22
2165
Одной из важнейших характеристик электромагнитного поля является его энергия. Впервые вопрос об энергии электромагнитного поля был рассмотрен Максвеллом, который показал, что полная энергия поля, заключенного внутри объема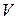 
, складывается из энергии электрического поля
и магнитного поля
Подынтегральные выражения здесь могут, таким образом, рассматриваться как плотности энергии электрического поля
и магнитного поля
.
Энергия электромагнитного поля, заключенного внутри объема 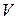, вообще говоря, не может оставаться постоянной. К числу факторов, обусловливающих изменение энергии поля во времени, следует отнести:
1. Превращение части энергии электромагнитного поля в энергию других видов, например, в механическую энергию частиц вещества, связанную с их тепловым движением, обусловленным протеканием токов проводимости.
2. Работу сторонних источников, которые, в зависимости от конкретных условий, могут как увеличивать запас энергии поля, так и уменьшать его.
3. Обмен энергией между выделенным объемом и окружающими его областями пространства за счет специфического процесса, присущего электромагнитному полю и носящему название процесса излучения.
Интенсивность процесса излучения в электродинамике принято характеризовать, определяя в каждой точке пространства особую векторную величину, носящую название вектора Пойнтинга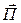 
. Физический смысл вектора Пойнтинга состоит в том, что его модуль и направление характеризуют величину и направление потока энергии излучения в каждой точке пространства. В системе единиц СИ вектор Пойнтинга имеет размерность 
. При этом полная убыль энергии электромагнитного поля, заключенного внутри воображаемого объема 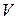с поверхностью 
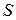, обусловленная излучением и отнесенная к единице времени, равна
На основании изложенного последний интеграл должен рассматриваться как величина мгновенной мощности излучения, происходящего по направлению из рассматриваемого объема в окружающее пространство. Если знак данного интеграла отрицателен, то это говорит о том, что поток энергии излучения направлен не из объема 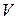, а внутрь него.
Физически правильные результаты, согласующиеся как с законом сохранения энергии, так и с уравнениями Максвелла, получаются в том случае, если выразить вектор Пойнтинга через мгновенные значения полей 
и 
следующим образом:
.
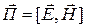Действительно, по теореме Остроградского-Гаусса для рассматриваемой замкнутой поверхности 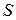будем иметь
.
Здесь было использовано известное тождество векторного анализа
.
С учетом уравнений Максвелла
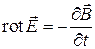
выражение примет вид
.
Интеграл вида
может быть назван мгновенной мощностью потерь, существующих внутри объема 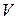за счет протекания токов проводимости. Другое слагаемое
характеризует мгновенную мощность, которая в зависимости от взаимной ориентации векторов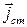 
и 
может либо вноситься в рассматриваемый объем, либо отводиться из него сторонними токами. Используя электротехнические термины, можно говорить о том, что источники стороннего тока способны выступать как в роли генераторов, так и в роли нагрузок. Наконец, если предположить, что между векторами поля в соответствии с материальными уравнениями существует линейная связь
, 
,
то последний интеграл в правой части формулы примет вид
.
Итак, на основании сказанного приходим к интегральному соотношению вида
,
являющемуся математическим выражением теоремы Пойнтинга. Это теорема устанавливает факт баланса энергий внутри произвольной области, в которой существует электромагнитное поле.
