Уравнения Максвелла являются линейными дифференциальными уравнениями, к ним может быть применен метод комплексных амплитуд. В этом случае вместо векторов электромагнитного поля рассматриваются комплексные векторы:
 ,
, 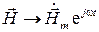 ,
,
и т.д. Тогда в первом уравнении Максвелла, например, получим:
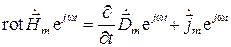 .
.
Поскольку постоянный множитель 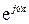 не зависящий от координат, выступает как постоянный коэффициент, а при дифференцировании по времени постоянной оказывается комплексная амплитуда, то
не зависящий от координат, выступает как постоянный коэффициент, а при дифференцировании по времени постоянной оказывается комплексная амплитуда, то
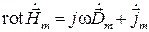 .
.
Таким образом, получено уравнение относительно комплексных амплитуд, утратившее временную зависимость. Аналогично для вектора 
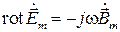
и

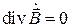 .
.
 2015-10-22
2015-10-22 1226
1226







