Уравнение линейной парной регрессии

Пусть между переменным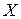и и 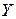теоретически существует некоторая линейная зависимость. Это утверждение может основываться на том, что корреляционное поле для пар имеет, например, такой вид (рис. 2)

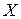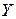Как видим, в действительности между признаками и наблюдается не такая тесная связь, как предполагает функциональная зависимость.

Отдельные наблюдаемые значения, как правило, отклоняются от ожидаемой линейной зависимости под воздействием случайных факторов, которые в большинстве неизвестны. Отклонения от ожидаемой линейной формы связи могут возникнуть вследствие неправильной спецификации уравнения, т.е. еще с самого начала неправильно выбрано уравнение, которое описывает зависимость между 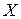и .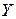

Допустим, что вид уравнения выбран правильно. Учитывая влияние на значения 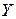возмущающих случайных факторов, линейное уравнение связ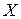и и 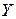можно представить в таком виде:

где и - неизвестные параметры регрессии;

- случайная величина, которая характеризует отклонение 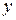от гипотетической теоретической регрессии.

В результате статистических наблюдений исследователь получает значения для независимой переменной 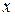и соответствующие значения зависимой переменной .

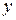Следовательно, необходимо определить параметры , . Но истинные значения этих параметров получить невозможно, т.к. мы пользуемся информацией, полученной от выборки ограниченного объема. Поэтому найденные значения параметров будут лишь статистическими оценками истинных (неизвестных нам) параметров , . Если обозначить параметры , , которые получили способом обработки выборки, то модели

соответствует статистическая оценка

На практике чаще всего параметры , определяются методом наименьших квадратов, разработка которого принадлежит К.Гауссу и П.Лапласу.

В соответствии с этим методом уравнение линейной регрессии необходимо выбрать так, чтобы сумма квадратов отклонений наблюдаемых значений от линии регрессии была бы минимальной