Корреляционный момент, выборочный коэффициент корреляции

Во время исследования двумерного статистического распределения выборки возникает необходимость выяснить наличие связи между признакам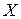и и 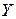, которую в статистике называют корреляционной. Для этого вычисляется эмпирический корреляционный момент по формуле

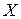Если , то корреляционной связи между признаками и 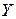нет. Если то эта связь существует.

Т.е. корреляционный момент дает лишь ответ на вопрос: есть связь между признакам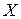и и 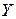или ее нет.

Для измерения тесноты корреляционной линейной связи вычисляется выборочный коэффициент корреляции 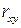по формуле

,

где . Чем ближе коэффициент корреляции к единице, тем корреляционная связь ближе к функциональной.

Задачи типа 441-450.

Õ Пример. Зависимость растворимости тиосульфата от температуры представлена парным статистическим распределением выборки

	33,5	37,0	41,2	46,1	50,0	52,9	56,8	64,3	69,9

Необходимо:

1. Построить корреляционное поле зависимости признака 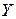от .
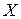2. Найти точечные статистические оценки 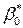, 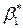для параметров 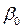, 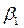парной линейной функции регрессии .
3. Вычислить выборочный коэффициент корреляции .
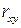4. Построить график линии регрессии.

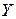Решение. 1. Корреляционное поле зависимости признака от 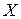имеет такой вид (рис. 3). Как видим, с увеличением признака , зависимая переменная имеет тенденцию к увеличению.

Допустим, что между признакам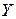и и 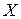существует линейная функциональная зависимость

.

2. Для определения параметров 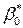, 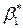составим следующую таблицу

№ п/п	хі	уі		хі уі
		33,5			1122,25
		37,0			1369,00
		41,2			1697,44
		46,1			2125,21
		50,0			2500,00
		52,9			2798,41
		56,8			3226,24
		64,3			4134,49
		69,9			4886,01
Σ		451,7			23859,05

Воспользуемся формулами

Так как n = 9,

получим

Следовательно, уравнение регрессии будет таким

3. Вычислим коэффициент корреляции по формуле

Как видим, коэффициент корреляции близок по своему значению к единице, что свидетельствует о том, что зависимость между 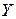и 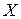практически линейная.

4. График парной линейной функции регрессии представлен на рис. 4. n