2015-10-22
1420
Случайная величина называется непрерывной, если ее возможные значения заполняют некоторый интервал полностью.
Интегральной функцией распределения называют функцию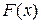 
, определяющую для каждого значения 
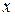вероятность того, что случайная величина 
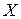примет значение, меньшее 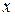, т.е.
.
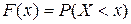Интегральная функция обладает следующими свойствами
Свойство 1. Значения интегральной функции принадлежат отрезку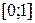 
.
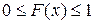Свойство 2. Интегральная функция есть неубывающая функция, т.е.
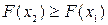, если 
.
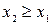Дифференциальной функцией распределения вероятностей называют первую производную от интегральной функции:
.
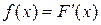Зная дифференциальную функцию, можно найти интегральную функцию по формуле:
.
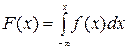Математическое ожидание непрерывной случайной величины 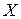, возможные значения которой принадлежат всей оси 
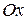, определяется равенством
,
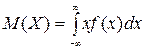где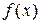 
–дифференциальная функция.
В частности, если все возможные знаения принадлежат интервалу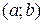 
, то
.
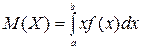Дисперсия непрерывной случайной величины 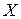, возможные значения которой принадлежат 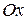, определяется равенством
|
|
|
,
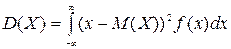или равносильным равенством
.
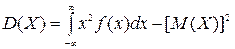В частности, если все возможные значения принадлежат интервалу 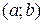, то
,
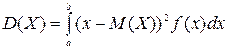или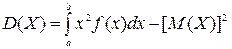 
.
Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины:
.
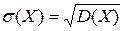Õ Пример. Случайная величина 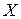задана интегральной функцией
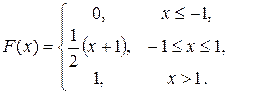
Найти дифференциальную функцию, математическое ожидание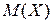 
и среднее квадратическое отклонение 
.
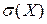Решение. Дифференциальную функцию найдем по формуле
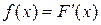
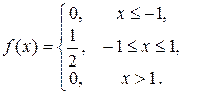
Найдем математическое ожидание
.
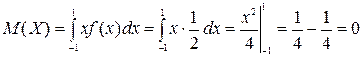Для вычисления дисперсии воспользуемся формулой
.
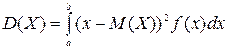Учитывая, что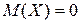 
получим
.
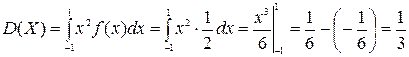Найдем искомое среднее квадратическое отклонение
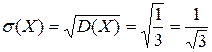n
