Закон Пуассона (закон редких явлений)

Пример. По мишени производится 4 независимых выстрела с вероятностью попадания при каждом выстреле р = 0,8. Требуется: а) найти закон распределения дискретной случайной величины х, равной числу попаданий в мишень; б) найти вероятности событий: 1 £ х £ 3; х > 3; в) построить многоугольник распределения.

Решение. а) Возможные значения случайной величины х: 0, 1, 2, 3, 4. Соответствующие вероятности вычисляем по формуле Бернулли:

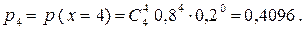
Биномиальный закон распределения х представится таблицей:

xi
pi	0,0016	0,0256	0,1536	0,4096	0,4096

Проверка: 0,0016 + 0,0256 + 0,1536 + 0,4096 + 0,4096 = 1.

б) Вероятность событий 1 £ х £ 3 и х > 3 равны:

р (1 £ х £ 3) = р ({1,2,3}) = р₁ + р₂ + р₃ = 0,0256 + 0,1536 + 0,4096 = 0,5888;

р(х > 3) = р ({4}) = р₄ = 0,4096.

Пример.

В урне 7 шаров, из которых 4 белых, а остальные черные. Из этой урны наудачу извлекаются 3 шара; х – число извлеченных белых шаров. Найдите закон распределения дискретной случайной величины х и вероятность события х ³ 2.

Решение.

Возможные значения случайной величины х: 0, 1, 2, 3. Соответствующие им вероятности р₀, р₁, р₂, р₃ подсчитываем классическим способом:

; ;

;

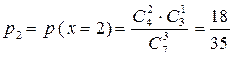Гипергеометрический закон распределения х:

xi
pi

Вероятность события х ³ 2 равна:

р (х ³ 2) = + = .

Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:

геометрический

xi				…	k	…
pi	p1	p2	p3	…	pk	…

где p_k = q^k-1p, q = 1 – p (0 < p < 1);

Закон распределения Пуассона:

xi					…	k	…
pi	p0	p1	p2	p3	…	pk	…

, l - положительное постоянное.

Закон распределения Пуассона является предельным для биномиального при n ® ¥, p ® 0, np = l = const. Виду этого обстоятельства при больших n и малых p биномиальные вероятности вычисляются приближенно по формуле Пуассона:

, где l = np.

Пример.

Завод отправил на базу 500 доброкачественных изделий. Вероятность повреждения каждого изделия в пути равна 0,002. Найдите закон распределения случайной величины х, равной числу поврежденных изделий, и найдите вероятности следующих событий:

А – повреждено менее 3 изделий;

В – повреждено более 2 изделий;

С – повреждено хотя бы одно изделие.

Решение.

Возможные значения х: 0, 1, 2,..., 500; так как n = 500 велико, а р = 0,002 мало, то положив l = 500 × 0,002 = 1, вычислим вероятности

p_k = p(x = k)

приближенно по формуле Пуассона:

, k = 0, 1, 2,..., 500.

Закон распределения случайной величины х приближенно имеет вид:

xk					…	500
pk					…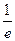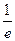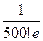

или

xk					…	500
pk	0,368	0,368	0,184	0,061	…	0,000

Используя полученную таблицу, находим вероятности событий А, В и С:

p(A) = p(x < 3) = p ({0, 1, 2}) = 0,368 + 0,368 + 0,184 = 0,92.

p(B) = p (x > 2) = 1 – p(x £ 2) 1 – p ({0, 1, 2}) = 0,008.

p(C) = p (x ³ 1) = 1 – p(x £ 0) 1 – p ({0}) = 1 – 0,368 = 0,632.