Лемма Чебышева. Если случайная величина х, для которой существует математическое ожидание М [ x ], может принимать только неотрицательные значения, то для любого положительного числа a имеет место неравенство
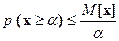 , (1)
, (1)
Неравенство Чебышева. Если х – случайная величина с математическим ожиданием М [ x ] и дисперсией D [ x ], то для любого положительного e имеет место неравенство
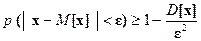 . (2)
. (2)
Теорема Чебышева. (закон больших чисел). Пусть х 1, х 2, …, xn,… - последовательность независимых случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же константой с. Тогда для любого положительного числа e имеет место предельное равенство
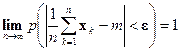 . (3)
. (3)
Доказательство теоремы основано на неравенстве
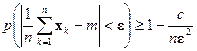 , (4)
, (4)
вытекающей из неравенства Чебышева. Из теоремы Чебышева как следствие может быть получена
Теорема Бернулли. Пусть производится n независимых опытов, в каждом из которых с вероятностью р может наступить некоторое событие А, и пусть vn – случайная величина, равная числу наступлений события А в этих n опытах. Тогда для любого e > 0 имеет место предельное равенство
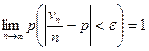 . (5)
. (5)
Отметим, что неравенство (4) применительно к условиям теоремы Бернулли дает:
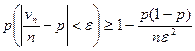 . (6)
. (6)
Теорему Чебышева можно сформулировать в несколько более общем виде:
Обобщенная теорема Чебышева. Пусть х1, х2, …, xn,… - последовательность независимых случайных величин с математическими ожиданиями M [ x 1] = m1, M [ x2 ] = m2,… и дисперсиями, ограниченными одной и той же постоянной с. Тогда для любого положительного числа e имеет место предельное равенство
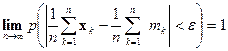 . (7)
. (7)
Пример.
Оцените вероятность того, что при 3600 независимых бросаниях игральной кости число появлений 6 очков будет не меньше 900.
Решение.
Пусть х -число появлений 6 очков при 3600 бросаниях кости. Тогда М [ x ] = 3600 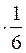 = 600. Воспользуемся теперь неравенством (1) при a = 900:
= 600. Воспользуемся теперь неравенством (1) при a = 900: 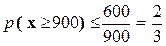 .
.
Пример.
Оцените вероятность того, что частота появления шестерки в 10000 независимых бросаниях игральной кости отклонится от вероятности появления шестерки по абсолютной величине меньше чем на 0,01.
Решение.
Используем неравенство (6) при n = 10000, р = 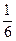 , q =
, q = 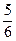 . Тогда
. Тогда
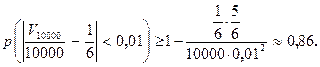
Пример.
Вероятность наступления события А в каждом из 1000 независимых опытов равна 0,8. Найдите вероятность того, что число наступлений события А в этих 1000 опытах отклонится от своего математического ожидания по абсолютной величине меньше чем на 50.
Решение.
Пусть х - число наступлений события А в указанных 1000 опытах. Тогда М [ x ] = 1000 × 0,8 = 800 и D [ x ] = 1000 × 0,8 × 0,2 = 160. Теперь неравенство (2) дает:
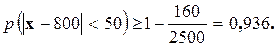
Пример.
Дисперсия каждой из 1000 независимых случайных величин xk (k = 1, 2,..., 1000) равна 4. Оцените вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий по абсолютной величине не превзойдет 0,1.
Решение:
Согласно неравенству (4) при с = 4 и e = 0,1 имеем:
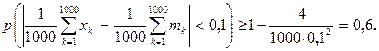
 2015-10-22
2015-10-22 7078
7078