«Введение в математический анализ»
«Дифференцирование функций одной переменной»
В состав расчетно-графической работы № 2 входят шесть заданий по темам, изучаемым во второй половине 1 семестра: вычисление предела функции, исследование на непрерывность элементарной функции, исследование на непрерывность неэлементарной функции, дифференцирование функции одной переменной, определение максимального и минимального значения функции одной переменной, построение графиков функций с полным исследованием.
Вариант 1.
1. Вычислить пределы функций:
а) 

б) 
 в)
в) 

г) 
 д)
д) 

2. Исследовать на непрерывность элементарную функцию
y = 
3. Исследовать на непрерывность неэлементарную функцию::
y= 
 <
<  <1, 1≤x≤2, x≥2
<1, 1≤x≤2, x≥2
4. Найти производную:
а) y = x sin(x ln x); б)  ;
;
в)  ; г)
; г)  ;
;
д)  ; е)
; е) 
5.Определить максимальное и минимальное значения функции
на отрезке  .
.


6.Построить графики функций:
а)  ; б)
; б)  .
.
Вариант 2.
1. Вычислить пределы функций:
а) 

б) 
 в)
в) 

г) 
 д)
д) 

2. Исследовать на непрерывность элементарную функцию:
y= 
3. Исследовать на непрерывность неэлементарную функцию:
y=  x<0, 0≤x<2, 2≤x≤3
x<0, 0≤x<2, 2≤x≤3
4. Найти производную:
а)  б)
б) 
в) 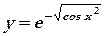 д)
д) 
г) 
5. Определить максимальное и минимальное значения функции на отрезке  .
.


6. Построить график функции.
а)  б)
б) 
Вариант 3
1. Вычислить пределы функций:
а) 

б) 
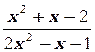
в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию:

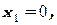

3. Исследовать на непрерывность неэлементарную функцию:
y=  x≤-1, -1<x<1, x≥1
x≤-1, -1<x<1, x≥1
4. Найти производную:
а)  в)
в) 
б) 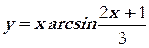 г)
г)  . д)
. д)  е)
е) 

 -?
-?  -?
-?
5. Определить максимальное и минимальное значения функции на отрезке  .
.

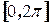
6. Построить график функции.
а)  б)
б) 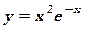
Вариант 4
1. Вычислить пределы функций:
а) 

б) 

в) 
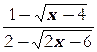
г) 

д) 

2. Исследовать на непрерывность элементарную функцию 


3. Исследовать на непрерывность неэлементарную функцию:
y=  x≤0, 0<x<2, x≥2
x≤0, 0<x<2, x≥2
4. Найти производную:
а) y=  г) y=
г) y= 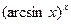
б) y=  д)
д) 
в) y=  е) y=
е) y= 
 ?,
?,  -?
-?
5. Определить максимальное и минимальное значения функции на отрезке  .
.


6. Построить график функции
а)  б)
б) 
Вариант 5
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию
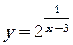
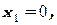

3. Исследовать на непрерывность неэлементарную функцию:
F(x) =  x≤0, 0<x<2, x≥2
x≤0, 0<x<2, x≥2
4. Найти производную:
а) y= 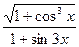 г)
г) 
б) y= 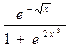 д) y=
д) y= 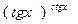
в) y=  е) y=
е) y= 
 -?,
-?,  ?
?
5.Определить максимальное и минимальное значения функции
на отрезке  .
.
y =  [-2,3]
[-2,3]
6. Построить график функции.
а) y=  б) y=
б) y= 
Вариант 6
1. Вычислить пределы функций:
а) 

б) 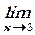

в) 

г) 

д) 

2. Провести полное исследование функций и построить их графики:
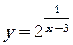


3. Исследовать на непрерывность неэлементарную функцию:
y=  x≤0, 0<x<3, x≥3
x≤0, 0<x<3, x≥3
4. Найти производную:
а) y= 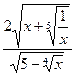 г) y=
г) y= 
б) y=  д)
д) 
в) y=  е) x=
е) x= 
 ?,
?,  ?
?
5. Определить максимальное и минимальное значения функции
на отрезке  .
.
y = x +  , [0,01, 100]
, [0,01, 100]
6. Построить график функции.
а) y =  б) y = lnsinx
б) y = lnsinx
Вариант 7.
1. Вычислить пределы функций:
а) 

б) 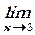

в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию:

3. Исследовать на непрерывность неэлементарную функцию:
y=  x<0, 0≤x<1, x≥1
x<0, 0≤x<1, x≥1
4. Найти производную:
а) y= 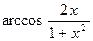 г) y=
г) y= 
б) y= 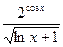 д) y =
д) y = 
в) y=  е) y=
е) y= 
5. Определить максимальное и минимальное значения функции
на отрезке  .
.
y = 2x-sinx [0,Π]
6. Построить график функции.
а) y = 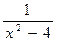 б) y =
б) y = 
Вариант 8
1. Вычислить пределы функций:
а) 

б) 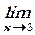

в) 
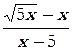
г) 

д) 

2. Исследовать на непрерывность элементарную функцию:



3. Исследовать на непрерывность неэлементарную функцию:
y= 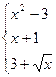 x<0, 0≤x≤4, x>4
x<0, 0≤x≤4, x>4
4. Найти производную:
а) y =  г) y=
г) y= 
б) y = 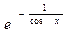 д) y=
д) y= 
в) y =ln  е)
е) 
 ?
?  -?
-?
5. Определить максимальное и минимальное значения функции на отрезке  .
.
y =sin3x-3sinx [0,  ]
]
6. Построить график функции.
y =  y = ln(x2+4x)
y = ln(x2+4x)
Вариант 9.
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию



3. Исследовать на непрерывность неэлементарную функцию:
y=  x≤1, 1<x≤3, x>3
x≤1, 1<x≤3, x>3
4. Найти производную:
а) y=  г)y=
г)y= 
б) y=  д)
д) 
в) y=  е)
е) 
 -?
-?  -?
-?
5. Определить максимальное и минимальное значения функции
на отрезке  .
.
y =  [0,2]
[0,2]
6. Построить график функции.
y =  y = xe-x
y = xe-x
Вариант 10.
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 
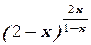
2. Исследовать на непрерывность элементарную функцию



3. Исследовать на непрерывность неэлементарную функцию:
y=  x<0, 0≤x≤4, x>4
x<0, 0≤x≤4, x>4
4. Найти производную:
а) y =  г) y = xe-x
г) y = xe-x
б) y =  д) exy-x2-y2 = 0
д) exy-x2-y2 = 0
в) y =  е) x = arctgt2, y = tsint
е) x = arctgt2, y = tsint  ?
?  ?
?
5. Определить максимальное и минимальное значения функции
на отрезке  .
.
y =  [0,
[0, 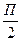 ]
]
6. Построить график функции.
а) y =  б) y =
б) y = 
Вариант 11
1. Вычислить пределы функций:
а) 
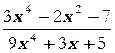
б) 

в) 

г) 
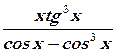
д) 

2. Исследовать на непрерывность элементарную функцию

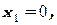

3. Исследовать на непрерывность неэлементарную функцию:
y= 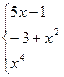 x≤0, 0<x≤2, x>2
x≤0, 0<x≤2, x>2 
4. Найти производную:
а) y =  г) y = (arcsin3x)
г) y = (arcsin3x) 
б) y =  д)
д) 
в) y =  е) y =
е) y = 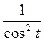 x=ctgt
x=ctgt  -?
-? 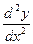 -?
-?
5. Определить максимальное и минимальное значения функции
на отрезке  .
.
y = 81x – x4 [-1,4]
6. Построить график функции.
а) y =  б) y =
б) y = 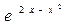
Вариант 12
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 
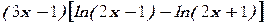
2. Исследовать на непрерывность элементарную функцию:



3. Исследовать на непрерывность неэлементарную функцию:
y=  x≤1, 1<x≤2, x>2
x≤1, 1<x≤2, x>2
4. Найти производную:
а) y=  г) y=
г) y= 
б) y=  д) y= xsiny-ycosx=0
д) y= xsiny-ycosx=0
в) y=  е) y=arctgt, x=tsint
е) y=arctgt, x=tsint  -?
-? 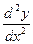 -?
-?
5. Определить максимальное и минимальное значения функции
на отрезке  .
.
y= x3 – 3x + 1 [0,3]
6. Построить график функции.
а)  б)
б) 
Вариант 13
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 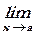

д) 

2. Исследовать на непрерывность элементарную функцию



3. Исследовать на непрерывность неэлементарную функцию:
y=  x<2, 2≤x≤3, x>3
x<2, 2≤x≤3, x>3
4. Найти производную:
а)  г) y=
г) y= 
б)  д)
д) 
в) 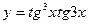 е) x=tcost,
е) x=tcost, 
 -?
-? 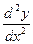 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке  .
.
y=x3(8-x) [0,1]
6. Построить график функции.
а)  б)
б) 
Вариант 14
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 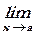

д) 

2. Исследовать на непрерывность элементарную функцию

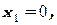

3. Исследовать на непрерывность неэлементарную функцию:
 x
x 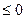 , 0<x≤2, x>2
, 0<x≤2, x>2
4. Найти производную:
а)  г)
г) 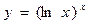
б)  д)
д) 
в)  е)
е) 

 -?
-? 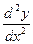 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке  .
.

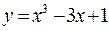 [-1,
[-1,  ]
]
6. Построить график функции.
а)  б)
б) 
Вариант 15
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 

2. Провести полное исследование функций и построить их графики:



3. Исследовать на непрерывность неэлементарную функцию:
 x≤0, 0<x≤2, x>2
x≤0, 0<x≤2, x>2 
4. Найти производную:
а) 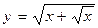 г)
г) 
б)  д)
д) 
в) 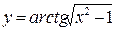 е)
е) 

 -?
-? 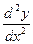 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a, b]
 [-2,0]
[-2,0]
6. Построить график функции.
а)  б)
б) 
Вариант 16
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 
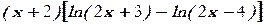
2. Исследовать на непрерывность элементарную функцию



3. Исследовать на непрерывность неэлементарную функцию:
 x≤0, 0<x≤1, x>1
x≤0, 0<x≤1, x>1
4. Найти производную:
а)  г)
г) 
б) 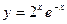 д)
д) 
в)  e)
e) 
 -?
-? 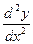 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a, b]


6. Построить график функции.
а)  б)
б) 
Вариант 17
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию

3. Исследовать на непрерывность неэлементарную функцию:

 <x<1, 1≤x<2, x≥2
<x<1, 1≤x<2, x≥2
4. Найти производную:
а)  г)
г) 
б)  д)
д) 
в) 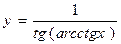 е)
е) 
 -?
-? 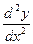 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a,b]

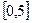
6.Построить график функции.
а)  б)
б) 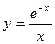
Вариант 18
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию:


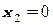
3. Исследовать на непрерывность неэлементарную функцию:
 x≤
x≤ 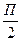 ,
, 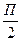 <x≤П, x≥П
<x≤П, x≥П
4. Найти производную:
а)  г)
г) 

б)  д)
д) 
в)  е)
е) 
 -?
-? 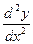 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a, b]
 [0,5]
[0,5]
6. Построить график функции.
а)  б)
б) 
Вариант 19
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д) 

2. Провести полное исследование функций и построить их графики:

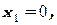

3. Исследовать на непрерывность неэлементарную функцию:
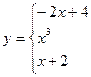 x ≤ -2, -2<x≤1, x>1
x ≤ -2, -2<x≤1, x>1
4. Найти производную:
а)  г)
г) 
б)  д)
д) 
в)  е)
е) 
 -?
-? 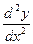 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a, b]


6. Построить график функции.
а)  б)
б) 
Вариант 20
1. Вычислить пределы функций:
а) 

б) 
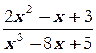
в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию



3. Исследовать на непрерывность неэлементарную функцию:
 x<0, 0≤x≤2, x>2
x<0, 0≤x≤2, x>2
4. Найти производную:
а)  г)
г) 
б) 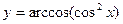 д)
д) 
в)  е)
е) 
 -?
-? 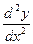 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a, b]

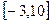
6. Построить график функции.
а)  б)
б) 
Вариант 21.
1. Вычислить пределы функций:
а) 

б) 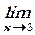

в) 

г) 

д) 

2. Исследовать на непрерывность элементарную функцию:
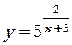


3. Исследовать на непрерывность неэлементарную функцию:
 x≤0, 0<x<
x≤0, 0<x< 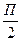 , x≥
, x≥ 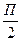
4. Найти производную:
а)  г)
г) 
б)  д)
д) 
в)  е)
е) 
 -?
-? 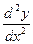 -?
-?
5. Определить максимальное и минимальное значения функции
на отрезке [a, b].
y=x3(8-x) [0,1]
6. Построить график функции.
а)  б)
б) 
Вариант 22.
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 

д)  (
( )
) 
2. Исследовать на непрерывность элементарную функцию



3. Исследовать на непрерывность неэлементарную функцию:
 x<0, 0
x<0, 0 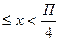 , x
, x 
4. Найти производную:
а) 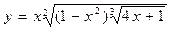 г)
г) 
б)  д)
д) 
в)  е)
е) 
 -?
-? 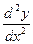 -?
-?
5. Определить максимальное и минимальное значения функции на отрезке [a, b]


6. Построить график функции.
а)  б)
б) 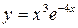
Вариант 23.
1. Вычислить пределы функций:
а) 

б) 

в) 

г) 


д)
 2015-10-22
2015-10-22 1732
1732








