1. Производная постоянной величины равна 0.
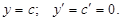
2. Производная алгебраической суммы нескольких дифференцируемых функций равна сумме производных этих функций.
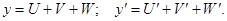
3. Производная произведения двух дифференцируемых функций равна сумме произведения каждой функции на производную другой функции.
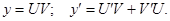
Следствия:
а) Постоянный множитель можно выносить за знак производной.
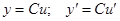
б) Производная произведения любого числа дифференцируемых функций равна сумме произведения производной каждой функции на произведение всех остальных функций.
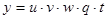 ;
; 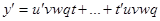
4. Производная частного равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя.
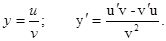
Следствия: 1) 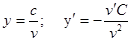 ; 2)
; 2) 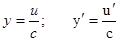 .
.
Производная сложной и обратной функции.
1. Производная сложной функции равна произведению производных от функций, составляющих данную функцию.
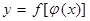 ,
, 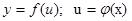 - дифференцируемые функции. Тогда
- дифференцируемые функции. Тогда
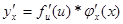 .
.
2. Производная обратной функции. Пусть нам дана дифференцируемая функция y = f(x). Если y рассматривать как аргумент, а x-функцию, то новая функция 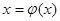 называется обратной по отношению к y. Зная производную функции y = f(x)
называется обратной по отношению к y. Зная производную функции y = f(x) 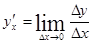 , можно найти производную обратной функции
, можно найти производную обратной функции 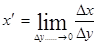 , предполагая, что обратная функция существует и непрерывна.
, предполагая, что обратная функция существует и непрерывна.
Теорема. Для дифференцируемой функции с производной не равной 0, производная обратной функции равна обратной величине производной данной функции 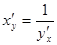 .
.
Таблица производных.
| № | Функция y | Производная 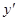 |
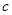 | ||
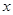 | ||
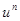 | 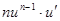 | |
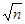 | 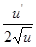 | |
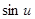 | 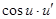 | |
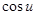 | 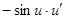 | |
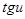 | 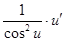 | |
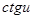 | 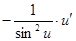 | |
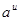 | 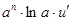 | |
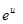 | 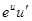 | |
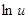 | 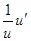 | |
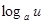 | 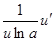 | |
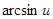 | 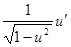 | |
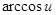 | 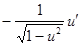 | |
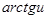 | 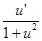 | |
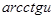 | 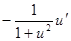 |
Примеры: Найти производную функций:
а) 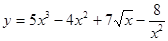
Воспользуемся формулами 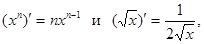 а также свойством производной, что постоянный множитель можно выносить за знак производной.
а также свойством производной, что постоянный множитель можно выносить за знак производной.
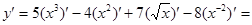
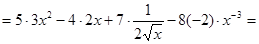
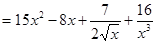 .
.
б) 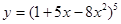
Это сложная степенная функция. Обозначим 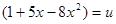 , тогда
, тогда 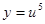 . Воспользуемся производной сложной функции.
. Воспользуемся производной сложной функции.
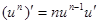
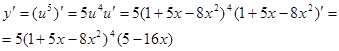
3. Производные высших порядков.
Производная у′ = f ′(x) называется производной первого порядка. Если f ′(x) дифференцируема, то ее производная обозначается символом у″ = f ″(x) и называется производной второго порядка.
Производная от производной первого порядка называется производной второго порядка.
Если 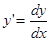 , то вторая производная обозначается
, то вторая производная обозначается
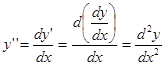 .
.
Производная n-го порядка есть производная от производной (n-1) порядка.
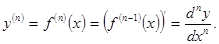
Пусть функция y = f(x) дифференцируема при некотором значении х. Следовательно, в точке х существует конечная производная 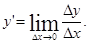 По определению предела имеем
По определению предела имеем 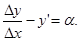
Отсюда находим 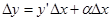 .
.
y′ от 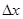 не зависит, она остается постоянной при
не зависит, она остается постоянной при 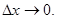
Если 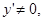 то
то 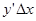 - является бесконечно малой величиной того же порядка малости, что и
- является бесконечно малой величиной того же порядка малости, что и 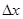 .
. 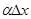 - бесконечно малая величина более высокого порядка малости, чем первое слагаемое. Поэтому величину
- бесконечно малая величина более высокого порядка малости, чем первое слагаемое. Поэтому величину 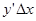 (
(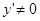 ) называют главной, линейной относительно
) называют главной, линейной относительно 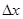 частью приращения функции; чем меньше
частью приращения функции; чем меньше 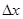 , тем большую долю приращения составляет это выражение. Поэтому при малых значениях
, тем большую долю приращения составляет это выражение. Поэтому при малых значениях 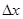 приращение функции можно заменить
приращение функции можно заменить 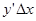 , т.е.
, т.е.
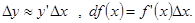
Эту главную часть приращения функции называют дифференциалом функции в точке х и обозначают dy или df(x), следовательно, 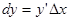 или
или 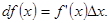
Дифференциал равен произведению ее производной на приращение независимой переменной.
Если f(x) = x, тогда dx = x′ 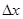 =
= 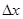 , т.е.
, т.е. 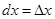 .
.
Окончательно можно записать: 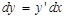
Из изложенного выше следует, что 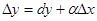 , т.е. приращение функции
, т.е. приращение функции 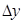 отличается от дифференциала
отличается от дифференциала 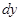 на бесконечно малую величину более высокого порядка, чем
на бесконечно малую величину более высокого порядка, чем 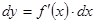 . Поэтому при достаточно малых значениях
. Поэтому при достаточно малых значениях 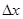 имеем
имеем 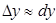 , т.е.
, т.е. 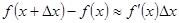 , откуда получаем формулу:
, откуда получаем формулу:
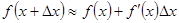 .
.
Чем меньше значение 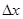 , тем точнее эта формула, и ее можно использовать для приближенных вычислений.
, тем точнее эта формула, и ее можно использовать для приближенных вычислений.
Пример. Вычислить 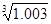
Решение: 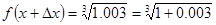 ,
,
где 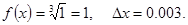
Найдем 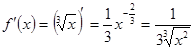 ,
, 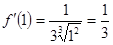 . Тогда имеем:
. Тогда имеем: 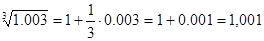
 2015-02-27
2015-02-27 24902
24902







