Швидкість та пропускна здатність акустичної інформаційної системи

Розглянемо модель обміну інформації по акустичному каналу в присутності завади. Припустимо що в акустичний канал випромінюється сигнал z(t) з середньою інтенсивністю(потужністю на одиницю поверхні) . В каналі діє адитивний гаусів білий шум - завада, з рівномірним частотним спектром і нормальним розподілом амплітуд, з середньою інтенсивністю(потужністю) . Статистичний зв'язок між сигналом і шумом відсутній, а ширина спектру сигналу і завади обмежена смугою пропускання інформаційної системи . Будемо вважати, що тривалість T сигналу досить велика, так що відповідно до теореми Котельникова можна замінити безперервні реалізації послідовностями з відліків, взятих з інтервалом: . Тоді середня кількість взаємної інформації в каналі у відповідності до (2.8) становить:

, (2.13)

де - апріорна та апостеріорна ентропії багатовимірного вектору повідомлення отриманого приймачем. Завада, за визначенням, адитивна і статистично незалежна з вхідним сигналом, тому використаємо наведене в [10] співвідношення:

. (2.14)

Ентропія N - мірного випадкового вектора завади, компонентами якого є випадкові величини у відповідних відліках безперервного гаусового білого шуму x (t), визначається:

, (2.15)

де - часткова ентропія одного відліку завади. Визначимо часткову ентропію для нормального процесу, заданого вірогідністю:

(2.16)

Ентропія для N - мірного випадкового вектора повідомлення визначається частковою ентропією одного відліку повідомлення :

(2.17)

Підставивши в (2.13) отримані значення апріорної та апостеріорної ентропій визначимо кількість взаємної інформації:

(2.18)

Інформаційна швидкість знаходиться з (2.11):

(2.19)

Як видно з (2.19) максимальну інформаційну швидкість, а значить і максимальну пропускну здатність каналу можна отримати максимізувавши

ентропією одного відліку повідомлення . Враховуючи те, що випромінений та прийнятий (випромінений сигнал що поступив на вхід приймача) сигнали є нормальним процесом та не мають статистичного зв’язку з завадою, запишемо середню потужність прийнятого сигналу у вигляді суми середніх потужностей вхідного сигналу і завади :

(2.20)

Підставимо співвідношення (2.20) в вираз для , який має ту ж форму що і вираз(2.16), отримаємо:

(2.21)

Пропускна здатність інформаційного акустичного каналу за наявністю завади з урахуванням (2.19), буде:

(2.22)

Визначимо залежність пропускної здатності каналу від частоти пропускання інформаційної системи 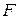. Середня потужність завади у полосі частот визначається через спектральну щільність потужності білого шуму 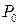рівнянням:

Підставимо його в (2.22), отримаємо:

, (2.23)

де . Розрахунок межі пропускної здатності для приведений в [10] наведено нижче:

(2.24)

Рис.2.1. відображає залежність пропускної здатності акустичного каналу.

Рис.2.1. Залежність пропускної здатності від частоти.

К. Шеннон застосував рівняння (2.22) для графічного представлення (рис.2.2) пропускної здатності каналу нормованої до частоти в залежності від рівня співвідношення сигнал /завада L, розрахованого як:

,дБ.