Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:
Таблица 2. Степени числа 2
| n | |||||||||||
|
Пример. Число  перевести в десятичную систему счисления.
перевести в десятичную систему счисления.

2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 3.4. Степени числа 8
| n | |||||||
|
Пример. Число  перевести в десятичную систему счисления.
перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 3. Степени числа 16
| n | |||||||

|
Пример. Число 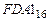 перевести в десятичную систему счисления.
перевести в десятичную систему счисления.
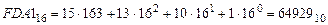
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число  перевести в двоичную систему счисления.
перевести в двоичную систему счисления.

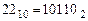
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число  перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.

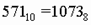
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число  перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.

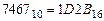
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число  перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.

8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число  перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.
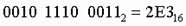
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Число 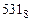 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
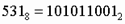
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число  перевести в двоичную систему счисления.
перевести в двоичную систему счисления.

11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число  перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.
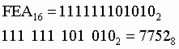
Пример 2. Число  перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.

1. Арифметические действия над целыми числами в 2-ой системе счисления:
1.Операция сложения выполняется с использованием таблицы двоичного сложения в одном разряде:
Пример.
а) +10012 б) +11012 в) +111112
10102 10112 12
100112 110002 1000002
2.Операция вычитания выполняется с использованием таблицы вычитания, в которой 1 обозначается заем в старшем разряде.
Пример.
а) –1011100112 б) –1101011012
1000110112 1010111112
0010110002 0010011102
3.Операция умножения выполняется по обычной схеме, применяемой в десятичной с/с с последовательным умножением множимого на очередную цифру множителя.
Пример.
а) ´ 110012 б) ´ 1012
11012 112
11001 101
11001 101
11001 11112
1010001012
4.Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в 10–ой с/с.
  Пример. Пример.
 1010001012 11012 1000110002 11112 1010001012 11012 1000110002 11112
 1101 110012 1111 100102
1110 10100
1101 1111
001101 10102 –остаток 1101 110012 1111 100102
1110 10100
1101 1111
001101 10102 –остаток
| 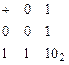

|
 2015-10-22
2015-10-22 589
589








