2015-10-22
330
Наиболее простым видом гармонических колебаний являются колебания математического маятника (Рис. 25.1) - колебания материальной точки, подвешенной на невесомой нити. Если вывести тело из состояния равновесия, то возникает результирующая сила 
,стремящаяся вернуть тело к прежнему положению. Запишем уравнение его движения. Т.к. сила 
направлена противоположно смещению маятника x, то:
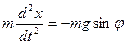(25.1)
Для малых углов отклонения 
и вместо (25.1) получим:
(25.2)
где
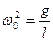(25.3)
Величина 
называется круговой или циклической частотой. Другой случай возникновения гармонических колебаний -колебания пружинного маятника (Рис. 25.2). Если вывести груз из положения равновесия, то со стороны пружины на него будет действовать возвращающая сила упругости F=-kx, где k- жесткость. Тогда 
или (25.4) где в этом случае 
(25.5)
Еще одним видом гармонических колебаний является колебание физического маятника - колебания тяжелого тела, колеблющегося вокруг оси, не проходящей через центр тяжести (Рис.25.3). Если центр тяжести расположен на расстоянии l от оси вращения в т.А, то момент силы тяжести равен:
M=mglsinφ
Этот момент заставляет отклоненный маятник вернуться в исходное состояние, поэтому уравнение его движения будет:
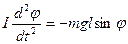(25.6)
где I - момент инерции маятника относительно оси вращения. Для малых отклонений 
. Получим:
(25.7) 
(25.8)
Как видно, во всех случаях гармонические колебания описываются уравнением одного вида (25.2), (25.4), (25.7). Решением такого уравнения является функция:
(25.9)
A=xmax называют амплитудой колебания, 
- фазой колебания, φ0 - начальная фаза.
Амплитуда и начальная фаза определяются начальными условиями - значениями смещения и скорости при t=0:x=x0, V=V0, где 
- скорость колебаний.
Т.к. гармонические колебания представляют периодический процесс о периодом Т, а период косинуса равен 2π, то из (25.9) находим:
, откуда:
или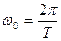 
(25.10)
С учетом этого из (25.3), (25.5), (25.8) находим периоды рассмотренных колебаний:
для математического маятника - 
пружинного -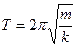 
физического - 
