2015-10-22
307
Кинетическая энергия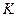 
равна разност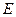и 
и 
:
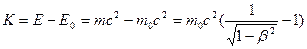(6.10)
При малых скоростях (
) 
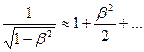и из формулы (6.10).получаем:
,
т.е. получим выражение для кинетической энергии в классической механике.
Исключив 
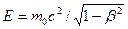ив выражений 
и 
, находим соотношение между импульсом и энергией:
, откуда 
(6.10)
Для частицы с массой покоя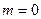 
(фотон) имеем:
КОЛЕБАНИЯ И ВОЛНЫ
| Лекция 8 | Малые колебания. Гармонический и ангармонический осциллятор. Уравнение гармонических колебаний. |
| Пружинный, физический и математический маятники. |
