2015-10-22
534
Поскольку значение скоростей молекул может быть бесконечно большое, а само число молекул ограниченно, то находят не число молекул, обладающих той или иной скоростью, а число молекул или их часть, обладающих скоростями, лежащими в некотором интервале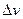 
вблизи заданной скорости 
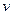. Например, число молекул, скорости которых лежат в пределах от 500 до 510 м/с (
).
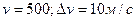Относительное число молекул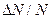 
, скорости которых лежат в интервале 
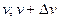, зависит од скорости V и тем больше, чем больше и 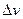, т.е.
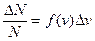(8.2)
функция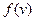 
называется функцией распределения. При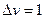 
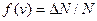, т.е. равна доле молекул, скорости которых заключены в единичном интервале скоростей. Так, как 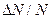имеет смысл вероятности, то 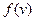- вероятность того, что молекула газа имеет скорость, заключенную в единичном интервале вблизи 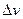. Можно графически представить зависимость 
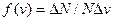от скорости 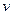. Число молекул 
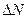, имеющих скорости 
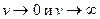, равны нулю.
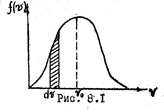
Поэтому искомая зависимость, как следует из математики, должна иметь максимум при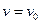 
и асимптотически приближаться к оси абсцисс при 
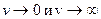(рис. 8.1). Аналитический вид ее для одинаковых молекул был рассчитан Максвеллом и. носит название закона распределения скоростей Максвелла:
|
|
|
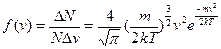(8.3)
Максимум этой функции при 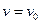означает, что наибольшая доля всех молекул движется со скоростями, близкими к 
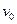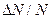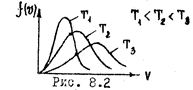
. Эту скорость поэтому называют наивероятной скоростью. Пользуясь кривой распределения, модно найти долю молекул , имеющих скорость в заданной интервале 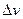.Она равна площади заштрихованной полосы. Вся же площадь под кривой дает полное число молекул я данном объёме. С повышением температуры скорости молекул возрастают, и кривая смещается в сторону больших скоростей (Рис. 8.2). Пользуясь (8.3) можно вычислить среднюю арифметическую 
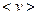и наивароятную скорость 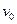. Вычисления дают:
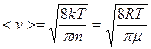(8.4); 
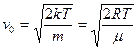(8.5)
Для решения практических задач удобно закон Максвелла (8.3) записывать через относительную скорость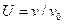 
. Из (8.5) и (8.3) можно получить:
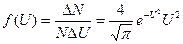(8.6)
В таком виде обычно пользуются законом Максвелла для решения задач, связанных с распределением молекул по скоростям. Экспериментальная проверка формулы распределения Максвелла впервые была проведена О. Штерном в 1920 г.
