Закон распределения Больцмана

Рассмотрим теперь влияние внешнего силового поля, например, силы тяжести на поведение молекул идеального газа. Если бы отсутствовало тепловое движение, то все молекулы под дейст­вием силы тяжести скопились бы у поверхности Земли, и, наобо­рот, в отсутствие силы тяжести все молекулы разлетелись бы по всему пространству. Одновременное действие обоих процессов и приводит к установлению определенного распределения молекул по высоте, соответственно чему распределяется и давление газа. Рассмотрим вертикальный столб газа (Рис. 8.3). При изменении высоты на давление меняется на . На некоторой высоте оно равно давлению столба газа:

(8.7)

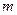где - плотность газа, - масса молекулы, - концентрация молекул. Из формулы (7.10). находим и 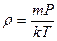. Под­ставив это в (8.7), получим: , откуда находим:

(8.8)

Так как 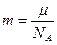, , то вместо (8.8) получим:

(8.9)

Формулы (8.8) и (8.9), устанавливающие закон убывания давления с высотой, называют барометрической формулой.

Так как давление газа пропорционально числу молекул, то (8.8) и (8.9) выражают также и закон убывания концентраций молекул:

(8.10)

Эта формула была использована Перроном (1909 г.) для опытней проверки барометрической формулы и числа Авогадро. В формуле (8.10) есть потенциальная энергия молекулы на высоте, то есть эта формула определяет число молекул (частиц) с энергией при нулевом уровне потенциальной энергии.

Если газ находится в другом силовом поле, так что его потенциальная энергия , то число частиц с такой энергией определится формулой:

(8.11)

Эту формулу называют формулой Больцмана.