| Представление | Описание |
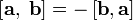 | свойство антикоммутативности |
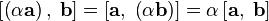 | свойство ассоциативности относительно умножения на скаляр |
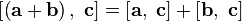 | свойство дистрибутивности по сложению |
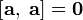 | |
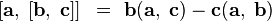 | формула «БАЦ минус ЦАБ», тождество Лагранжа |
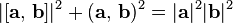 | |
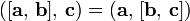 | значение этого выражения (число) называют смешанным произведением векторов a, b, c и обозначают (a, b, c) либо <a, b, c> |
Модуль векторного произведения [ a, b ] равняется площади S параллелограмма, построенного на приведённых к общему началу векторах a и b (см. Рисунок) Если e — единичный вектор, ортогональный векторам a и b и выбранный так, что тройка (a, b, e) — правая, а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула: 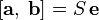 | 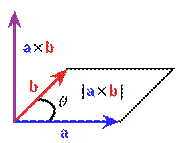 |
Свойства векторного произведения
|
|

Сейчас читают про:
 2015-10-22
2015-10-22 847
847







