Ортогональные системы векторов

Определение 1. Система векторов евклидова пространства { } называется ортогональной, если все ее элементы попарно ортогональны:

Теорема 1. Ортогональная система неравных нулю векторов линейно независима.

{Предположим, система линейно зависима: и, для определенности, Умножим скалярно равенство на 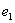. Учитывая ортогональность системы, получим: }

Определение 2. Система векторов евклидова пространства { } называется ортонормированной, если она ортогональна и норма каждого элемента равна единице.

Из теоремы 1 сразу следует, что ортонормированная система элементов всегда линейно независима. Отсюда, в свою очередь, следует, что в n – мерном евклидовом пространстве ортонормированная система из n векторов образует базис (например, { i, j, k } в 3 ^х – мерном пространстве).Такаясистема называется ортонормированным базисом, а ее векторы – базисными ортами.

Координаты вектора в ортонормированном базисе можно легко вычислить с помощью скалярного произведения: если Действительно, умножая равенство на , получаем указанную формулу.

Вообще, все основные величины: скалярное произведение векторов, длина вектора, косинус угла между векторами и т.д. имеют наиболее простой вид в ортонормированном базисе. Рассмотрим скалярное произведение: , так как

а все остальные слагаемые равны нулю. Отсюда сразу получаем: ,

* Рассмотрим произвольный базис 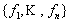. Скалярное произведение в этом базисе будет равно:

(Здесь α_i и β _j – координаты векторов в базисе { f }, а – скалярные произведения базисных векторов).

Величины γ_ij образуют матрицу G, называемую матрицей Грама. Скалярное произведение в матричной форме будет иметь вид: *

Теорема 2. В любом n – мерном евклидовом пространстве существует ортонормированный базис. Доказательство теоремы носит конструктивный характер и носит название