С помощью средств программной среды MathCADможностроитьграфики видов:
· двумерные
· трехмерные.
Рассмотрим построение двумерных графиков. Эту задачу можно решить двумя способами:
· путем использования интервальной переменной;
· путем использования интервальной переменной и переменной с индексами.
В первом случае сначала определяется функция. Для этого вводится имя функции, затем в скобках ее аргументы, далее оператор присваивания. После этого вводится ее алгебраическое выражение. После этих операций определенная таким образом функция может использоваться наравне со встроенными функциями. Например, введем параболическую функцию:

Заметим, что все параметры, входящие в функцию, должны быть заданы до определения функции.
Чтобы получить значение функции при определенном значении аргумента необходимо записать:

и т.д.
Для построения графика функции необходимо многократно вычислять ее значения при различных значениях аргумента. Для этого в программе MathCAD предусмотрено понятие интервальной переменной (по аналогии с понятием циклов в языках программирования). Синтаксис интервальной переменной имеет вид:
:=начальное значение[, начальное значение+шаг]..конечное значение
В скобках указан необязательный параметр шаг, по умолчанию равный 1. Двоеточие <..> вводится клавишей точка с запятой <;> или кнопкой <m..n> панели Матрица.
Допустим, что аргумент функции х изменяется на отрезке [-2;2] с шагом h=1. С помощью интервальной переменной это записывается следующим образом:
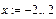
Чтобы получить значения аргумента (интервальной переменной), введем: х=. Для получения значений функции введем: f(x)=. Полученные значения аргумента и функции показаны на рисунке 1.

Рисунок 1
Для построения графика воспользуемся панелью Графика, в которой выберем
Х-У график. В маркере оси х укажем переменную х, в маркере оси у – переменную у. График будет иметь вид, показанный на рисунке 2.
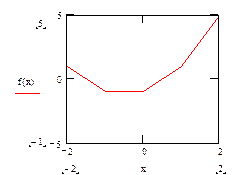
Рисунок 2
Выделив график двойным щелчком, можно производить настройку графика, в частности выбрать тип, цвет, толщину линии и т.д. Можно, например, использовать опции графической панели:
· Zoom - позволяет выделить часть графика;
· Trace – отслеживает изменение координат на графике и т.д.
Пусть шаг изменения аргумента будет равен 0,1. Интервальная переменная в этом случае будет иметь вид:
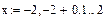
Тогда график примет вид, показанный на рисунке 3.
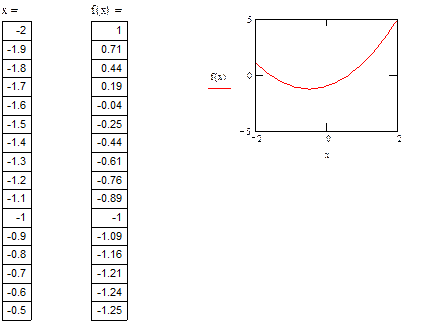
Рисунок 3
Чтобы просмотреть все значения функции и аргумента надо щелкнуть мышкой по соответствующей таблице и воспользоваться появившейся линейкой прокрутки.
Рассмотрим второй способ построения графиков – путем использования интервальной переменной и переменной с индексами. Построим тот же график этим способом.
Введем индекс как интервальную переменную:

Определим xi:
xi:=-2+0,1+i
Вычислим:

То есть, получим вектор-столбец значений функции. Введем х= и у=, получим матрицы. При помощи переменной с индексом созданы две одномерные матрицы с одним столбцом и 41-й строкой. Теперь строим график, где в качестве аргумента и функции следует указать переменные с индексом хi и yi.
На одном Х-У графике можно построить до 16 функций. Функции вводятся через запятую.
Аналогично можно использовать двумерную матрицу для построения графика функции двух переменных. Например, определим функцию от двух переменных и две интервальные переменные:
f(x,y):=x2-y2
i:=0..10 j:=0..10
Теперь определяем две переменные с индексом:
xi:=-5+0,1+i yj:=-5+0,1+j
Определим двумерную матрицу:
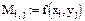
и построим поверхность, выбрав на панели Графика соответствующую кнопку. В качестве единственного аргумента графика укажем имя матрицы М.
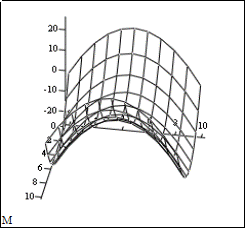
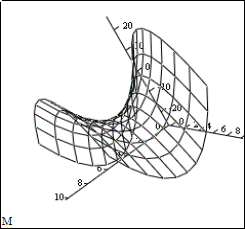
Рисунок 4 Рисунок 5
Изменив настройки можно получить другое изображение поверхности, как показано на рисунке 5. Для этого двойным щелчком мыши вызываем меню настройки и устанавливаем опции цвета, поворот -50 градусов и угол зрения 35.
Задания.
Построить график функции одной переменной двумя способами и график функции двух переменных. Интервал изменения аргументов от –5 до 4 с шагом 0,5. График функции одной переменной построить в декартовых и полярных координатах.
| Номер варианта | Двумерный график | Трехмерный график |
| 1. | 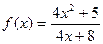 | 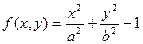 |
| 2. | 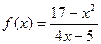 | 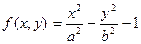 |
| 3. | 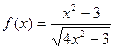 | 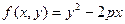 |
| 4. | 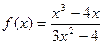  | 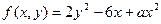 |
| 5. | 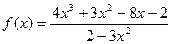 | 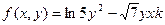 |
| 6. | 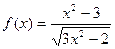 | 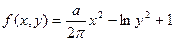 |
| 7. | 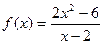 | 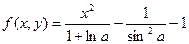 |
| 8. | 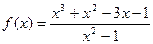 |  |
| 9. | 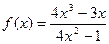 | 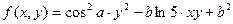 |
| 10. | 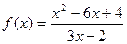 | 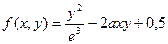 |
| 11. | 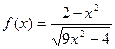 | 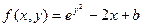 |
| 12. | 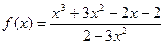 | 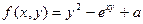 |
| 13. | 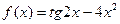 | 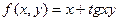 |
| 14. | 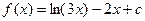 | 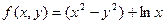 |
| 15. | 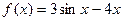 | 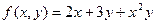 |
| 16. | 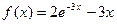 |  |
| 17. | 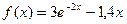 | 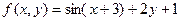 |
| 18. |  | 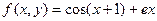 |
| 19. | 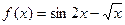 | 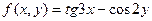 |
| 20. | 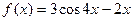 |  |
| 21. | 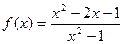 | 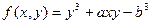 |
| 22. | 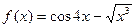 | 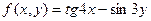 |
| 23. | 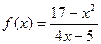 | 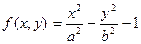 |
| 24. | 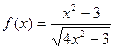 | 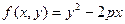 |
| 25. | 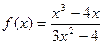  | 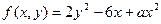 |
| 26. | 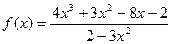 | 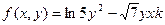 |
| 27. | 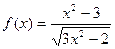 | 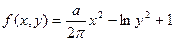 |
| 28. | 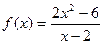 | 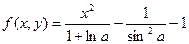 |
| 29. | 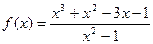 |  |
| 30. | 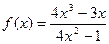 | 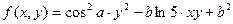 |
| 31. | 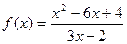 | 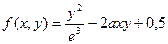 |
| 32. | 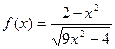 | 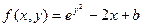 |
| 33. | 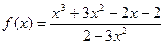 | 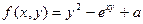 |
| 34. | 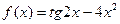 | 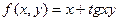 |
| 35. | 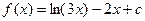 | 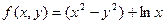 |
| 36. | 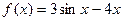 | 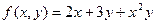 |
| 37. | 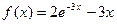 |  |
| 38. | 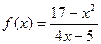 | 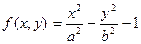 |
| 39. | 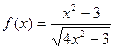 | 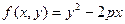 |
| 40. | 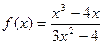  | 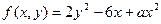 |
| 41. | 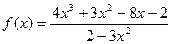 | 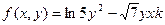 |
| 42. | 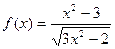 | 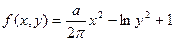 |
 2015-10-22
2015-10-22 1152
1152
