Матрица – это прямоугольная таблица чисел (массив). Матрицы бывают одномерные и двумерные. Одномерная матрица – это массив, состоящий из одного столбца. Матрица создается с помощью команды Вставка/Матрица, затем указывается количество строк и столбцов.
Например, создадим две матрицы размерностью 3х3 и 3х1:

Матрица с одним столбцом называется вектор-столбцом. Матрицы принято обозначать прописными латинскими буквами.
Матрицы можно умножать, складывать, вычислять определитель матрицы, транспонировать матрицу, находить обратную матрицу и производить многие другие вычисления матричной алгебры.
Например:
1. Умножение матрицы на число:
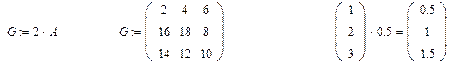
2. Сложение матриц:

Сложение матриц начинается с набора знака суммирования <+>, умножение - знака умножения <*>. Известно, что при сложении размеры матриц должны совпадать.
Доступ к элементам матриц осуществляется с помощью механизма индексирования. В одномерной матрице все значения пронумерованы от 0 до n-1, где n – количество значений. Обращение к элементу матрицы производится по номеру, который называется индексом. Например, в матрице В имеется три значения с индексами 0,1,2 и обращение к ним производится как к переменной с индексом:
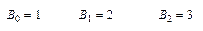
Индекс вводится с помощью символа квадратной скобки или из панели Калькулятор. Заметим, что переменные с индексами могут присутствовать в арифметических выражениях наряду с другими переменными.
Элементы двумерных массивов задаются указанием через запятую двух индексов: первый индекс – это номер строки матрицы, второй – номер столбца. Как и в одномерных матрицах, нумерация начинается с 0. Например:

Задания.
Ввести матрицу и выполнить действия:
· Вычислить определитель матрицы А.
· Транспонировать матрицу А.
· Найти обратную матрицу А.
· Умножить матрицу А на диагональную единичную матрицу той же размерности.
· Определить ранг матрицы А.
· Возвести матрицу А в указанную cтепень (степенью является номер варианта).
· Вычесть из матрицы А матрицу А, приведенную в следующем номере варианта, т.е. из матрицы А (номер варианта 1) вычесть матрицу А (номер варианта 2), из матрицы А (номер варианта 2) вычесть матрицу А (номер варианта 3) и т.д. из матрицы А (номер варианта 22) вычесть матрицу А (номер варианта 1).
· Сложить с матрицей А матрицу А, приведенную в следующем номере варианта (методика сложения происходит по аналогии с предыдущим заданием).
| Номер варианта | Матрица А | Номер варианта | Матрица А |
| 1. |  | 2. |  |
| 3. |  | 4. |  |
| 5. |  | 6. |  |
| 7. |  | 8. |  |
| 9. |  | 10. |  |
| 11. |  | 12. |   |
| 13. |  | 14. |  |
| 15. |  | 16. |  |
| 17. |  | 18. |  |
| 19. |  | 20. |  |
| 21. |  | 22. |  |
| 23. |  | 24. |  |
| 25. |  | 26. |  |
| 27. |  | 28. |  |
| 29. |  | 30. |  |
| 31. |  | 32. |  |
| 33. |  | 34. |  |
| 35. |  | 36. |   |
| 37. |  | 38. |  |
| 39. |  | 40. |  |
| 41. |  | 42. |  |
 2015-10-22
2015-10-22 1224
1224
