Для численного поиска корней уравнения в программе MathCAD используется функция root. Она служит для решения уравнений вида f(x) = 0, где f(x)— выражение, корни которого нужно найти, а x — неизвестное. Для поиска корней с помощью функции root, надо присвоить искомой переменной начальное значение, а затем вычислить корень при помощи вызова функции: root (f(x),x). Здесь f(x) — функция переменной х, используемой в качестве второго параметра. Функция root возвращает значение независимой переменной, обращающее функцию f(x) в 0. Например:
х:= 1
root(2-sin(x) – x,x) = 1,895.
Если уравнение имеет несколько корней (как в данном примере), то результат, выдаваемый функцией root, зависит от выбранного начального приближения.
Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом функции find (найти). Между ними располагают «логические утверждения», задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения.
Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства — кнопка Логически равно на панели инструментов Логика. Другие знаки логических условий также можно найти на этой панели.
Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечислены искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных. Например:
х:= 0 у:= 0
given
x+y=1
х2 + у2=4
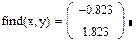
Задания.
Решить уравнение и систему уравнений, приведенных в таблице. Начальное значение х=0. Систему линейных уравнений решить двумя способами: методом, описанным выше и с помощью матриц коэффициентов С=А-1×В. Выполнить проверку ответов с помощью подстановки.
| Номер варианта | Уравнение | Система уравнений |
| 1. |  | 5x+8y-z=-7 x+2y+3z=1 2x-3y+2z=9 |
| 2. |  | x+2y+2=4 3x-5y+3z=1 2x+7y-z=8 |
| 3. |  | 3x+2y+z=5 2x+3y+z=1 2x+y+3z=11 |
| 4. |  | х+2y+4z=51 5x+y-2z=29 3x-y+z=10 |
| 5. |  | 4x—3y+27=9 2x+5y-3z=4 5x+6y-2z=18 |
| 6. |  | 2x-y-z=4 3x+4y-2z=11 3x-2y+4z=11 |
| 7. |  | x+y+2z=-1 x-y+2z=-4 4x+y+4z=-2 |
| 8. |  | 3x-y+z=5 -2x+y+z=0 2x-4y+4z=2 |
| 9. |  | 3x-y+z=4 2x-5y-3z=-17 x+y-z=1 |
| 10. |  | x+y+z=2 2x-y-8z=-1 3x-2y+z=8 |
| 11. |  | 2x+y+z=1 x+y+z=6 3x-y+z=4 |
| 12. |  | 2x-y-3z=3 3x+4y-5z=8 x+2y+7z=12 |
| 13. |  | x+5y+z=-7 2x-y-z=0 x-2y-z=2 |
| 14. | 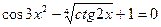 | x-2y+3z=6 2x+3y-4z=8 3x-2y-5z=12 |
| 15. |  | 1,84x+2,25y+2,53z=-6,09 2,32x+2,6y+2,82z=-6,98 1,83x+2,06y+2,24z=-5,52 |
| 16. |  | 2,58x+2,93y+3/13z=-6,66 1,32x+1,55y+1,58z=-3,58 2,09+2,25y+2,34z=-5,01 |
| 17. |  | 2,18x+2,44+2,49z=-4,34 2,17x+2,31y+2,49z=-3,91 3,15x+3,22y+3,17z=-5,27 |
| 18. |  | 1,54x+1,7y+1,62z=-1,97 3,69x+3,73y+3,59z=-3,74 2,45x+2,43y+2,25z=-2,26 |
| 19. |  | 1,53x+1,61y+1,43z=-5,13 2,35x+2,31y+2,07z=-3,69 3,83x+3,73y+3,45z=-5,98 |
| 20. |  | 2,36x+2,37y+2,13z=1,48 2,51x+2,4y+2,1z=1,92 2,59x+2,41y+2,06z=2,16 |
| 21. | 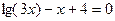 | 5x3+8y2+7=0 x+2y-1=0 |
| 22. |  | x2+2y4+6=0 3x-y+2=0 |
| 23. |  | 5x+8y-z=-7 x+2y+3z=1 2x-3y+2z=9 |
| 24. |  | x+2y+2=4 3x-5y+3z=1 2x+7y-z=8 |
| 25. |  | 3x+2y+z=5 2x+3y+z=1 2x+y+3z=11 |
| 26. |  | х+2y+4z=51 5x+y-2z=29 3x-y+z=10 |
| 27. |  | 4x—3y+27=9 2x+5y-3z=4 5x+6y-2z=18 |
| 28. |  | 2x-y-z=4 3x+4y-2z=11 3x-2y+4z=11 |
| 29. |  | x+y+2z=-1 x-y+2z=-4 4x+y+4z=-2 |
| 30. |  | 3x-y+z=5 -2x+y+z=0 2x-4y+4z=2 |
| 31. |  | 3x-y+z=4 2x-5y-3z=-17 x+y-z=1 |
| 32. |  | x+y+z=2 2x-y-8z=-1 3x-2y+z=8 |
| 33. |  | 2x+y+z=1 x+y+z=6 3x-y+z=4 |
| 34. |  | 2x-y-3z=3 3x+4y-5z=8 x+2y+7z=12 |
| 35. |  | x+5y+z=-7 2x-y-z=0 x-2y-z=2 |
| 36. | 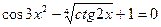 | x-2y+3z=6 2x+3y-4z=8 3x-2y-5z=12 |
| 37. |  | 1,84x+2,25y+2,53z=-6,09 2,32x+2,6y+2,82z=-6,98 1,83x+2,06y+2,24z=-5,52 |
| 38. |  | 5x+8y-z=-7 x+2y+3z=1 2x-3y+2z=9 |
| 39. |  | x+2y+2=4 3x-5y+3z=1 2x+7y-z=8 |
| 40. |  | 3x+2y+z=5 2x+3y+z=1 2x+y+3z=11 |
| 41. |  | х+2y+4z=51 5x+y-2z=29 3x-y+z=10 |
| 42. |  | 4x—3y+27=9 2x+5y-3z=4 5x+6y-2z=18 |
 2015-10-22
2015-10-22 2063
2063
