Іі. Похибки непрямих (опосередкованих) вимірювань

При фізичних дослідженнях часто доводиться оперувати величинами, що виміряні не безпосередньо, а обчислені за результатами прямих вимірювань інших величин. Похибка кінцевого результату, в цьому випадку, залежить як від похибок прямих вимірювань, так і від характеру тих формул, за допомогою яких проводиться обчислення.

Похибка суми

Нехай деяка фізична величина х знаходиться додаванням двох виміряних величин а і b. Тоді:

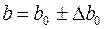
1. Абсолютна похибка визначається наступним чином:

х=а+b=а₀ 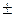Δ а₀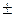+b₀ Δ b₀.

Тоді: Δ х₀=х–х₀=а₀ 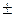Δ а₀+b₀ 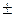Δ b₀–а₀–b₀,

або: Δ х₀= 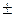(Δ а₀+ Δ b₀).

Отже: абсолютна похибка суми дорівнює сумі абсолютних похибок доданків.

2. Відносна похибка суми визначається за формулою:

.

Похибка різниці

Якщо деяка фізична величина х знаходиться як різниця двох виміряних величин а і b, то:

х = а – b,

х₀ = а₀ – b₀.

1. Отримаємо формулу для визначення абсолютної похибки різниці:

.

У цій формулі записали замість (повинно бути: 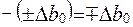) тому, що ці два записи рівноцінні.

Тоді:

,

або:

.

Тобто: абсолютна похибка різниці дорівнює сумі абсолютних похибок зменшуваного і від’ємника.

2. Відносна похибка різниці більша відносної похибки суми і дорівнює:

.

Похибка добутку

Нехай і , тоді:

1. Абсолютна похибка:

.

Доданок є величиною вищого порядку малості, тому ним можна знехтувати.

Тоді:

,

або:

.

2. Відносна похибка:

,

або

ε = %.

Тобто: відносна похибка добутку дорівнює сумі відносних похибок співмножників вимірюваних величин.

Похибка частки

Нехай і .

1. Абсолютна похибка.

.

Оскільки 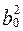>> 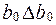, то:

.

2. Відносна похибка

Тобто: відносна похибка частки дорівнює сумі відносних похибок чисельника і знаменника.

Похибка степеня

У попередніх прикладах за відомою абсолютною похибкою знаходили відносну:

.

Інколи зручніше спочатку визначити відносну похибку ε, а потім абсолютну :

= .

Розглянемо цей метод на прикладі похибки степеня.

Використовуючи метод математичної індукції, можна легко узагальнити правило знаходження відносної похибки степеня.

Нехай:

, тобто: .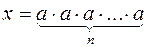

Тоді: ε= .

Таким чином, відносну похибку степеня знаходять за формулою:

ε = .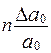

Отримаємо формулу для знаходження абсолютної похибки степеня:

.

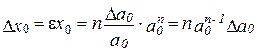Тобто:

.

Похибка кореня

Якщо , то це можна записати як степінь:

.

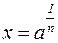Використовуючи отримані вище формули для знаходження відносної і абсолютної похибок степеня для кореня маємо:

ε і

.