Оптимальне керування. Принцип максимуму Понтрягіна
Література: [5, с. 421-489], [6, с. 13-85].
Мета роботи: Навчитися застосовувати принцип максимуму Понтрягіна до знаходження оптимального керування динамічними системами.
Зміст роботи: Розв’язати запропоновану задачу пошуку оптимального керування, використовуючи принцип максимуму Понтрягіна. Скласти програму для графічного відображення поведінки системи під дією розрахованого керування однією з алгоритмічних мов.
Методичні вказівки
Основна задача. Нехай задана динамічна система

 (5.1)
(5.1)
.................

або у векторній формі  ,
, 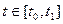 з початковою умовою
з початковою умовою  і областю допустимих керувань
і областю допустимих керувань  . Тут
. Тут  –
– 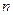 -вимірний вектор, який називають фазовим, а його компоненти – фазовими координатами об’єкта, функції
-вимірний вектор, який називають фазовим, а його компоненти – фазовими координатами об’єкта, функції  мають частинні похідні
мають частинні похідні  (
( і неперервні разом з цими похідними за сукупністю своїх аргументів. Шукається таке допустиме керування і відповідна траєкторія системи (5.1), щоб для фіксованого скінченного моменту часу
і неперервні разом з цими похідними за сукупністю своїх аргументів. Шукається таке допустиме керування і відповідна траєкторія системи (5.1), щоб для фіксованого скінченного моменту часу  вираз
вираз
 , (5.2)
, (5.2)
де  - задані сталі, був мінімальним.
- задані сталі, був мінімальним.
Нехай 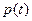 – вектор-функція з компонентами
– вектор-функція з компонентами  , яка є розв’язком задачі
, яка є розв’язком задачі
 ,
,  ,
,  , (5.3)
, (5.3)
або у векторній формі  ,
,  , де
, де
 ,
, 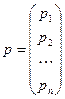 ,
,  .
.
Система (5.3) називається приєднаною до системи (5.1).
Функція Гамільтона задач (5.1),(5.2) має вигляд
 .
.
Тоді динамічна і приєднана системи можуть бути записані через канонічні рівняння
 ,
, 
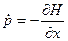 ,
,  .
.
Теорема. Нехай  – розв’язок задачі (5.1),(5.3). Тоді існує функція
– розв’язок задачі (5.1),(5.3). Тоді існує функція 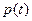 , яка є розв’язком приєднаної системи (5.3) з відповідною граничною умовою і така, що майже для всіх
, яка є розв’язком приєднаної системи (5.3) з відповідною граничною умовою і така, що майже для всіх 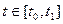 виконується умова
виконується умова
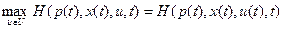 .
.
Якщо необхідно мінімізувати двічі диференційовну за всіма аргументами функцію  , то в принципі максимуму Понтрягіна початкові умови для приєднаної системи треба замінити на
, то в принципі максимуму Понтрягіна початкові умови для приєднаної системи треба замінити на  .
.
Якщо ставиться задача мінімізації функціоналу  , де функція
, де функція  задовольняє ті ж умови, що й
задовольняє ті ж умови, що й  , то функція Гамільтона визначається формулою
, то функція Гамільтона визначається формулою  , а приєднана система має вигляд
, а приєднана система має вигляд
 ,
, 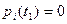 ,
,  . (5.4)
. (5.4)
Приклад 5.1. 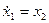 ,
, 
 ,
,  ,
,  ,
, 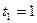 ,
,  .
.
Розв’язання.  ,
,  ,
,  ,
,  ,
,  , тобто
, тобто  . Звідси
. Звідси  . Максимум
. Максимум  досягається при
досягається при  .
.
Умови трансверсальності. Часто у задачі (5.1),(5.2) накладаються умови вигляду  ,
,  , причому вважається, що функції
, причому вважається, що функції  двічі диференційовні по всіх
двічі диференційовні по всіх  і якобіан
і якобіан  має максимальний ранг
має максимальний ранг  . Тоді умови
. Тоді умови 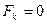 ,
,  задають у просторі станів деякий гладкий многовид.
задають у просторі станів деякий гладкий многовид.
Вимагається знайти таке оптимальне керування, яке переводить точку  у довільну точку цього многовиду. В цьому випадку кінцеві умови для
у довільну точку цього многовиду. В цьому випадку кінцеві умови для  в принципі максимуму Понтрягіна потрібно замінити умовами трансверсальності
в принципі максимуму Понтрягіна потрібно замінити умовами трансверсальності
 ,
,  .
.
Приклад 5.2. 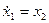 ,
,  ,
, 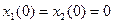 ,
,  ,
,  .
.
Розв’язання. Маємо 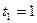 ,
,  ,
,  ,
,  ,
,  ,
, 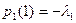 ,
,  ,
, 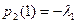 , тобто
, тобто  і
і  . Звідси, максимум функції Гамільтона дає оптимальне керування
. Звідси, максимум функції Гамільтона дає оптимальне керування 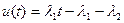 . Невідомі параметри
. Невідомі параметри 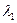 і
і  потрібно вибрати так, щоб система переводилась у кінцеву точку
потрібно вибрати так, щоб система переводилась у кінцеву точку  . Інтегруючи рівняння стану, одержуємо
. Інтегруючи рівняння стану, одержуємо
 ,
,
З умов  легко записати лінійні рівняння для знаходження
легко записати лінійні рівняння для знаходження 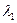 і
і  :
:  ,
,  , так що оптимальне керування має вигляд
, так що оптимальне керування має вигляд  .
.
Аналогічно одержують умови трасверсальності для початкової точки у випадку, коли 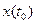 не задано, а лише вимагається, щоб ця точка задовольняла систему
не задано, а лише вимагається, щоб ця точка задовольняла систему  ,
, 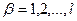 . Тоді для приєднаної вектор-функції має виконуватись умова
. Тоді для приєднаної вектор-функції має виконуватись умова 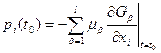 ,
,  .
.
Завдання для самостійної роботи
Розв’язати наведені нижче задачі. Розробити алгоритми і скласти програму для графічного відображення поведінки системи під дією розрахованого керування.
1. 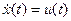 ,
, 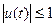 ,
,  ,
,  ,
, 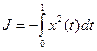 .
.
2. 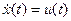 ,
,  ,
,  ,
,  .
.
3.  ,
,  ,
,  ,
,  .
.
4.  ,
,  .
. 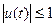 ,
,  ,
,  ,
,  ,
,  ,
, 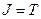 .
.
5.  ,
,  ,
,  ,
,  ,
,  .
.
6.  ,
,  ,
, 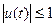 ,
,  ,
, 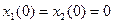 ,
,  .
.
7.  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
8.  ,
,  ,
,  ,
,  ,.
,.
9.  ,
,  ,
,  ,
,  .
.
10.  ,
,  ,
,  ,
, 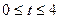 ,
,
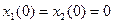 ,
,  .
.
11.  ,
, 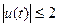 ,
,  ,
,  ,
,  ,
,  ,
, 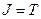 .
.
12. 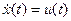 ,
, 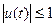 ,
,  ,
,  ,
,  .
.
13. 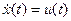 ,
, 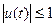 ,
,  ,
,  ,
,  .
.
14. 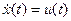 ,
, 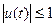 ,
, 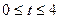 ,
,  ,
,  .
.
15. 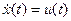 ,
, 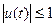 ,
,  ,
,  ,
,  .
.
16. 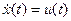 ,
, 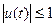 ,
,  ,
,  ,
,  .
.
17.  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
18.  ,
,  ,
,  ,
,  ,
, 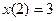 ,
,  .
.
19.  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
20.  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
21.  ,
,  ,
,  ,
,  ,
,  .
.
22.  ,
,  ,
,  ,
,  ,
,  .
.
23. 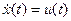 ,
, 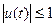 ,
,  ,
,  ,
,  .
.
24. 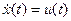 ,
,  ,
,  ,
,  .
.
25.  ,
,  ,
,  ,
,  ,
,  .
.
26.  ,
,  ,
,  ,
,  ,
,  .
.
27.  ,
,  ,
,  ,
, 
28.  ,
, 
 ,
,  ,
,  ,
,  ,
, 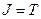 .
.
Література
1. Александров А.Г. Оптимальные и адаптивные системы. – М.: Высшая Школа, 1989. – 263 с.
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986. – 544 с.
3. Бублик Б.Н., Кириченко Н.Ф. Основы теории управления. - К.: Вища школа, 1975. - 328 с.
4. Гантмахер Ф.Р. Теория матриц. - М.: Наука, 1967. - 576 с.
5. Васильев Ф.П. Численные методы решения экстремальных задач. – М.: Наука, 1998. – 552 с.
6. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. – М.: Наука, 1983. – 392 с.
 2015-10-22
2015-10-22 307
307







