2015-10-22
240
Керування дискретними лінійними системами
Література: [3, c.108-112].
Мета роботи: Застосувати теоретичні критерії дослідження керовності дискретних лінійних систем до розробки алгоритмів розрахунку управління для переведення їх у наперед заданий стан.
Зміст роботи: Дослідити, чи є цілком керовною задана дискретна лінійна система керування. Розрахувати управління для її переведення у наперед заданий стан, використовуючи програмні засоби одного з пакетів Maple, Mathcad чи Matlab.
Методичні вказівки
Розглянемо дискретну лінійну систему керування вигляду
, (4.1)
де 
— 
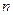-вимірний вектор стану системи в точці 
, 
— вектор керування в точці 
, 
і 
- деякі матриці, елементи яких залежать від дискретного аргументу у випадку нестаціонарної системи і не залежать від у випадку стаціонарної системи.
Теорема. Для того, щоб лінійна дискретна система (4.1) була цілком керовною на проміжку від 
до 
, необхідно і досить, щоб виконувалась умова:
(4.2)
.
При цьому керування, яке переводить систему із стану 
в стан 
знаходиться як розв’язок системи лінійних алгебраїчних рівнянь
(4.3)
.
У випадку стаціонарних дискретних систем керування умова керовності набуде вигляду
(4.4)
Якщо матриця 
у стаціонарній системі складається з одного стовпця, то умова (4.3) зводиться до нерівності
.
При цьому система (4.3) запишеться так:
.
Завдання для самостійної роботи
Для заданих матриць 
і 
дискретної стаціонарної лінійної системи керування обчислити керування, яке за п’ять кроків переводить систему із стану з усіма нульовими компонентами у стан з усіма одиничними компонентами. Для проведення відповідних розрахунків можна використати один із пакетів Maple, Mathcad чи Matlab.
Варіанти матриць і ті ж самі, що й у попередній роботі.
