2015-10-22
624
1.Уравнение состояния идеального газа (уравнение Менделеева-
Клапейрона)
где p, V – давление и объём, занимаемый данной массой газа; m, 
– масса и молярная масса газа; R – универсальная газовая постоянная;
T – термодинамическая температура 
К; t – температура по шкале Цельсия; 
– количество вещества.
2. Для смеси газов справедлив закон Дальтона
где 
– парциальное давление 
компонента смеси; k – число компонентов смеси.
3.Основное уравнение молекулярно-кинетической теории газов
или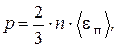 
где 
– масса одной молекулы; n – концентрация молекул; 
– средняя квадратичная скорость молекул; 
– средняя кинетическая энергия поступательного движения молекул.
4. Средняя кинетическая энергия молекулы (с учётом поступательного и вращательного движений)
где i – число степеней свободы (для одноатомной молекулы i= 3 ( пост .); для двухатомной молекулы i= 5 (3 пост. + 2 вращ.); для трех- и более атомной молекулы i= 6 (3 пост.+ 3 пост.)); k – постоянная Больцмана.
5. Скорость молекул:
средняя квадратичная
средняя арифметическая
,
наиболее вероятная
; 
.
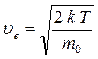6. Зависимость давления газа от концентрации молекул и температуры
7. Теплоёмкость системы (тела)
,
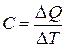где 
– количество теплоты, сообщённое системе (телу);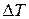 
– изменение температуры системы (тела), вызванное сообщением этого количества теплоты.
8. Молярная и удельная теплоёмкости
; 
.
9. Молярные теплоёмкости идеального газа при постоянном объёме 
и постоянном давлении 
; 
.
10. Соотношение между молярной и удельной теплоёмкостями
11. Удельные теплоёмкости при постоянном объёме 
и постоянном давлении С P уд
СV уд 
; С Р уд 
.
12. Отношение теплоёмкостей (показатель адиабаты)
13. Внутренняя энергия идеального газа массой m при температуре Т
14. Первое начало термодинамики
где Q – количество теплоты, сообщённое газу в рассматриваемом процессе;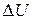 
– изменение внутренней энергии в данном процессе;
А – работа газа над внешними силами.
15. Работа, совершаемая газом, при изменении его объёма
где 
, 
и 
– начальный и конечный объём соответственно.
16. Для любого процесса, происходящего с идеальным газом, изменение внутренней энергии рассчитывается по одной и той же формуле
.
17. Количество теплоты и работа, совершаемая газом, зависит от вида процесса.
• Изотермический процесс: T= const; 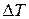= 0; 
;
.
• Изохорический процесс: V= const;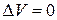 
; 
;
.
• Изобарический процесс Р = const;
, 
• Адиабатный процесс – процесс, при котором отсутствует теплообмен между системой и окружающей средой:
Q адиаб = 0,
А адиаб = 
или
А адиаб = 
,
где γ– показатель адиабаты.
18. КПД тепловой машины:
• любой
• идеальной, работающей по циклу Карно
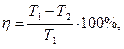
где А – полезная работа; 
и 
– соответственно количество теплоты, полученное от нагревателя и отданное холодильнику; 
и 
– соответственно температуры нагревателя и холодильника.
19. Средняя длина свободного пробега молекул газа
где d – эффективный диаметр молекулы; n – концентрация молекул в единице объёма.
Пример 1.
В сосуде 
л содержится 10 г азота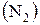 
и 20 г углекислого газа 
при 
К. Определить молярную массу смеси и давление смеси до и после её нагревания до температуры 400К.
Дано: л = 
; 
г = 0,01 кг; 
г = 0,02 кг; К.
Найти: р; ; р/ (T / = 400 K).
Решение:
Согласно закону Дальтона
(1)
Запишем парциальные давления газа азота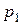 
и углекислого газа 
, используя уравнение состояния:
, (2)
(3)
Согласно таблице Менделеева Д.И.
г/моль = 28∙10 –3 кг/моль
г/моль = 44∙10 –3 кг/моль
Подставив (2) и (3) в (1), получим
Выполним вычисления p до нагревания6
Па.
Молярная масса смеси
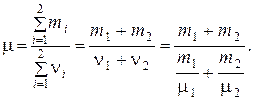
Выполним вычисления :
кг/моль.
Так как объём смеси не изменяется, то уравнение состояния газа можно записать в виде
Тогда
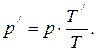
Найдем давление смеси после её нагревания:
Па.
Ответ: 
Па; 
кг/моль; 
Па.
Пример 2. Найти КПД тепловой машины работающей по циклу, состоящего из двух изохор и двух изобар, если известно что 
Дж/(К∙моль).
Дано: 
; 
; Дж/(К∙моль).
Найти: 
.
Решение:
Изобразим цикл, по которому работает тепловая машина в координатах 
(рис. 1).
 |
Рис. 1
Согласно рис.1 
По определению КПД
Работа тепловой машины за цикл численно равна площади фигуры, ограниченной кривой цикла. В данной задаче работа численно равна площади прямоугольника. Тогда
так как 
Используя уравнение состояния 
, выражение для работы газа примет вид:
(1)
В процессах 1–2 и 2–3 рабочее тело получает количество теплоты, так как с газом происходит изохорное нагревание и изобарное расширение. Тогда
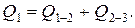
В процессах 3 – 4 и 4 – 1 рабочее тело машины отдаёт количество теплоты, так как с газом происходит изохорное охлаждение и изобарное сжатие.
Распишем 
согласно изопроцессам
(2)
Используя уравнение состояния 
, определим температуры 
и 
:
1) в процессе 1 – 2 (V 1 = V 2 Þ изохорный процесс)
или 
; (3)
2) в процессе 2 – 3 (Р 2 = Р 3 Þ изобарный процесс)
или учитывая, что V 3 = 2× V 2 получим
(4)
Молярные теплоёмкости в изобарном и изохорном процессах:
(5)
Подставим (3), (4), (5) в (2):
(6)
Подставим (6) и (1) в выражение для определения :
Выполним вычисления:
или 
.
Ответ: .
ЭЛЕКТРОСТАТИКА
