2015-10-22
446
,
где 
так как среда воздух, 
– сторона квадрата;
где 
;
Подставим уравнения для сил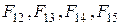 
в выражение (2):
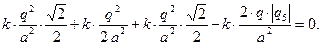(3)
Преобразуем выражение (3), найдя общий знаменатель:
(4)
Выражение (4) верно, если числитель равен 0:
(5)
Из выражения (5), найдем величину заряда 
:
Произведём вычисления
Кл.
Ответ: 
Кл = – 96∙10 – 9 Кл = – 96 нКл.
Пример 4. Электрическое поле создано зарядами 
нКл и 
нКл, находящимися на расстоянии 10 см. Определить напряжённость и потенциал поля в точке, удалённой от первого заряда на 12 см, а от второго на 6 см.
Дано: нКл = 
Кл; нКл = 
Кл;
; 
см = 0,12 м;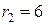 
см = 0,6 м.
Найти: 
Решение: В соответствии с условием задачи изобразим вектора напряжённостей, созданные зарядами q 1 и q 2 в точке А (рис. 4):
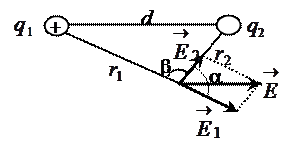
Рис. 4
Согласно принципу суперпозиции
Используя теорему косинусов, перейдём от векторной формы к скалярной:
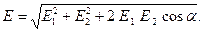(1)
Напряжённость электрического поля, создаваемого точечными зарядами 
и 
на расстояниях 
и 
, соответственно равны:
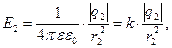
так как 
Определим значение 
из треугольника со сторонами 
, , d, используя теорему косинусов (рис. 10):
|
|
|
Таким образом,
Произведём расчёт 
:
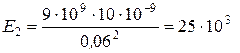Н/Кл,
Н/Кл.
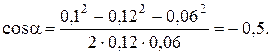
Для расчёта результирующего значения напряжённости Е подставим значения 
в формулу (1):
Н/Кл.
Так как поле создаётся двумя точечными зарядами, то потенциал в рассматриваемой точке следует искать методом суперпозиции. В соответствии с этим
где 
– потенциалы в рассматриваемой точке, созданные зарядами и соответственно.
Используя формулу потенциала поля, создаваемого точечным зарядом, получим:
Выполним вычисления:
В.
Ответ: 
Н/Кл, 
=1500 В.
ПОСТОЯННЫЙ ТОК
