Рассмотрим систему из двух уравнений первого порядка:
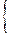 a11 х1 + a12 х2 = b1
a11 х1 + a12 х2 = b1
a21 х1 + a22 х2 = b2
Выделим из этой системы три определителя: определитель самой системы D= 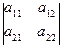 , определитель для первого неизвестного D1=
, определитель для первого неизвестного D1= 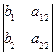 , определитель для второго неизвестного D2=
, определитель для второго неизвестного D2= 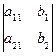 . Обратим внимание, что индексы у определителей для неизвестных будут теперь соответствовать номеру неизвестного в системе. Рассмотрим три возможных случая:
. Обратим внимание, что индексы у определителей для неизвестных будут теперь соответствовать номеру неизвестного в системе. Рассмотрим три возможных случая:
1. Определитель системы D 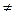 0. Тогда имеем единственное решение х1 =
0. Тогда имеем единственное решение х1 = 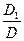 , х2 =
, х2 = 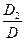 (формулы Крамера для двух неизвестных).
(формулы Крамера для двух неизвестных).
2. D=D1=D2=0. В этом случае система имеет бесконечное множество решений.
3. D=0, но D1 или D2, или оба вместе, не равны нулю. В этом случае система несовместна, т.е. не имеет никаких решений.
Совершенно аналогично строятся формулы Крамера для систем более высокого порядка. Так, для трех уравнений:
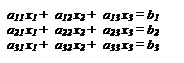
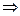 D=
D= 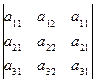 , D1=
, D1= 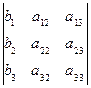 , D2=
, D2= 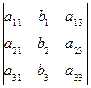 ,
,
 D3=
D3=  .
.
Тогда, если D  0, то единственное решение определится формулами хi =
0, то единственное решение определится формулами хi = 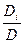 (i =1, 2, 3).
(i =1, 2, 3).
Так же, как и при вычислении определителей, формулы Крамера, из-за арифметических трудностей, используются на практике для систем не выше третьего - четвертого порядков.
Матрицы
Определения
Матрицей А называется прямоугольная таблица чисел, имеющая m строк и n столбцов, т.е. размерность m 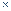 n (m, n
n (m, n 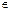 N). Примеры:
N). Примеры:
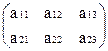
А 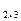 = =
= = 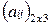 - прямоугольная;
- прямоугольная;
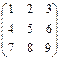
А 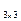 = - квадратная;
= - квадратная;
А 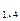 =
= 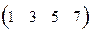 - строка (или: матрица-строка);
- строка (или: матрица-строка); 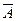 = А
= А 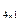 =
= 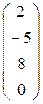 - вектор (или: матрица-столбец); Е =
- вектор (или: матрица-столбец); Е = 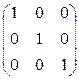 - единичная (всегда квадратная); А д =
- единичная (всегда квадратная); А д = 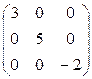 - диагональная (тоже всегда квадратная).
- диагональная (тоже всегда квадратная).
Квадратная матрица называется симметричной, если a 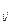 =a
=a 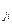 при i
при i 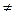 j.
j.
Заметим, что матрица качественно отличается от определителя. Матрица - не число, а нераздельное множество чисел, представленное в виде таблицы. Только квадратные матрицы можно связать с определителями, которые в этом случае будут иметь статус некоторой полезной характеристики при операциях с квадратными матрицами.
Матрицы имеют большое практическое значение, т.к. многие объекты и процессы проще всего описывать именно матрицами.
 2015-10-22
2015-10-22 333
333








