Степень и функции матриц

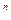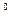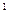Для квадратных матриц целая степень матрицы определяется так же, как и для обычных чисел: А =А А А ... А (n сомножителей). При этом полагается: А =Е; А =А.

В целом ряде случаев необходимо использовать отрицательную степень матрицы. Она может быть введена по правилу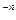: А = (А ) .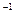

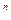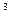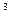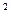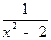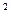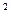С помощью этих формул можно решать задачи типа: если известен закон изменения f(x), то: определить f (A) - функцию от матрицы. Например, если f(x)= 2x -3x+5, то f (A)= 2 A -3 A +5 E. Если f(x)= 4 x + , то f (A)=4 A +(A -2 E) .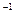

Ясно, что матрица А должна быть такой, чтобы все операции имели смысл. Единичная матрица Е использована для формального преобразования обычных чисел к матричной записи. По размерности она должна соответствовать матрице А.