Рівняння площини у відрізках

Якщо в загальному рівнянні

жодне з чисел не дорівнює нулю, то площину можна побудувати за трьома точками перетину її з координатними осями:

, де відрізки, які відтинає площина на координатних осях (див. рис. 12).

Рис.12

Рівняння площини у відрізках запишеться:

Прямі називаються слідами даної площини на координатних площинах – відповідно. Їх рівняння можна отримати із загального, якщо в останньому прирівняти до нуля відповідну змінну. Так, наприклад, якщо (площина 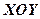), то в цій площині рівняння сліда запишеться

.

Аналогічно для інших слідів.

Приклади.

1.Побудувати площину і записати її рівняння у відрізках, а також рівняння слідів на відповідних координатних площинах.

Розв’язання. Покладемо , тоді

. Аналогічно при знаходимо , при , тоді рівняння у відрізках запишеться

Рис. 13.

Рівняння слідів:

2. Знайти об’єм піраміди обмеженої площиною та координатними площинами.

Відповідь: .

3.Знайти площу трикутника, який відтиняється координатними площинами від площини .

Відповідь: .