Пряма лінія і площина

Кут між прямою і площиною

Нехай пряма і площина 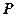задані відповідно своїми рівняннями

і

Кутом між прямою та площиною 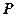називається кут, утворений цією прямою і її проекцією на площину 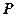(рис. 23).

Позначимо через величину цього кута. Кут між нормальним вектором і напрямним вектором дорівнює кутові , тому . Отже,

Рис. 23.

З рис. 23 видно, що , коли

– умова паралельності прямої і площини.

І якщо , то

– умова перпендикулярності прямої і площини.

Приклади

1. Знайти кут між прямою і площиною .

Розв’язання. Відповідно до формули (31) з першого рівняння знаходимо напрямний вектор з рівняння площини – нормальний вектор тоді

2. Скласти рівняння площини, яка проходить через точку А(-3,4,-7) і перпендикулярна прямій

Розв’язання. Відповідно умові (33) перпендикулярності прямої і площини за нормальний вектор площини можна взяти паралельний йому напрямний вектор прямої Використовуючи рівняння площини, яка проходить через точку А(-3,4,-7) перпендикулярно вектору маємо