1. Дано точки 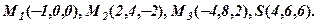 Скласти рівняння площини
Скласти рівняння площини  та знайти висоту
та знайти висоту  піраміди
піраміди 
2. Знайти точку перетину трьох площин

Вказівка. Розв’язати систему рівнянь.
3. Побудувати площини: 1)  2)
2)  3)
3)  4)
4)  5)
5) 
4. Скласти рівняння площини, яка перпендикулярна осі ОУ і проходить через точку М(-6,7,10).
5. Написати рівняння площини, яка проходить через вісь ОХ і точку М(4,-5,6).
6. Написати рівняння площини, яка паралельна осі OZ і проходить через точки М(-1,4,-8) і N(2,-3,-1).
7. Записати рівняння площини  у відрізках.
у відрізках.
8. Знайти об’єм піраміди, утвореної координатними площинами та площиною  .
.
9. Дано площину  . Необхідно знайти: 1) об’єм піраміди, обмеженої цією площиною та координатними площинами; 2) відстань до цієї площини від початку координат; 3) площу бічної грані, яка відтинається координатними площинами від заданої площини.
. Необхідно знайти: 1) об’єм піраміди, обмеженої цією площиною та координатними площинами; 2) відстань до цієї площини від початку координат; 3) площу бічної грані, яка відтинається координатними площинами від заданої площини.
10. Дві грані куба лежать на площинах  і
і  .
.
11. Скласти рівняння геометричного місця точок, рівновіддалених від двох площин  і
і 
12. Знайти гострий кут між площинами  і
і 
13. Дано вершини піраміди А(1,-2,2), В(2,-3,-6), С(5,1,4) і  . Знайти довжину висоти, яка проведена із вершини В.
. Знайти довжину висоти, яка проведена із вершини В.
14. Скласти рівняння площини, яка проходить через точки  і В(1,-2,8) і перпендикулярна площині
і В(1,-2,8) і перпендикулярна площині  .
.
Відповіді: 1. 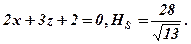 2.
2. 
4. у-7=0. 5. 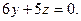 6.
6.  7.
7. 
8. 96. 9. 1) 243; 2) 6; 3) 121,5. 10. 8. 11. 
12. 60°. 13. 4. 14. 
Пряма в просторі
3.15. Канонічне та параметричне рівняння прямої в просторі
Аналогічна задача вже розв’язувалась для прямої на площині. Отже, необхідно скласти рівняння прямої  , що проходить через дану точку
, що проходить через дану точку  паралельно напрямному вектору
паралельно напрямному вектору 
Нехай, 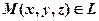 – довільна точка прямої, тоді вектори
– довільна точка прямої, тоді вектори  і
і  колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
колінеарні, а це значить, що координати їх пропорційні, тому отримуємо
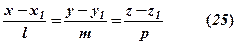
– канонічні рівняння прямої. Прирівнюючи кожний з дробів (25) до параметра 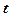 , запишемо параметричні рівняння прямої
, запишемо параметричні рівняння прямої

Приклад. За точкою М(1,5,2) і напрямним вектором 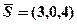 необхідно: 1) скласти канонічне рівняння прямої
необхідно: 1) скласти канонічне рівняння прямої  ; 2) побудувати цю пряму.
; 2) побудувати цю пряму.
Розв’язання. 1) За формулою (25) запишемо канонічне рівняння прямої  :
:

2) Розглянемо два способи побудови прямої  .
.
Перший спосіб. В системі координат XYZ будуємо вектор  і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору
і точку М(1,5,2) і проводимо через точку М пряму паралельну вектору 
Другий спосіб. За формулою (26) записуємо рівняння прямої  в параметричному вигляді:
в параметричному вигляді:

 При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій
При довільних значеннях t із системи знаходимо координати відповідних точок, які належать прямій  . Так при t=1 знаходимо координати М1(4,5,6). Через дві точки М і М1 проводимо пряму
. Так при t=1 знаходимо координати М1(4,5,6). Через дві точки М і М1 проводимо пряму  (див. Мал.)
(див. Мал.)
Задачі.
1. На прямій  знайти точки, які знаходяться на відстані 10 одиниць від точки
знайти точки, які знаходяться на відстані 10 одиниць від точки 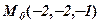 .
.
Відповідь:  .
.
2. Точка 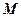 рухається рівномірно з величиною швидкості
рухається рівномірно з величиною швидкості  м/с в напрямку вектора
м/с в напрямку вектора  від початкової точки
від початкової точки 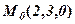 . Знайти координати точки
. Знайти координати точки 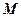 через
через  с від початку руху.
с від початку руху.
Відповідь: 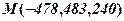 .
.
Вказівка. Скористатись методикою відповідних задач, розв’язаних в 3.7.
 2015-10-22
2015-10-22 511
511








