Пусть любыми соседними узлами сетки 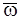 функция y(x) интерполируется кубическим полиномом S3(x). Его коэффициенты на каждом интервале определяются из условий:
функция y(x) интерполируется кубическим полиномом S3(x). Его коэффициенты на каждом интервале определяются из условий:
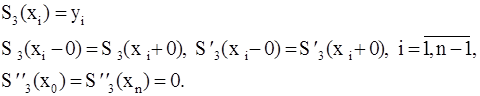 . .
| (6.11) |
Ищем кубический сплайн S3(x) в виде
| S3(x) = ai + bi (x – xi-1) + ci (x – xi-1)2 + di (x – xi-1)3, | (6.12) |
xi-1 £ x £ xi.
Требуя, чтобы S3(x) из (6.12) удовлетворял условиям (6.11), получим для коэффициентов 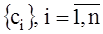 трехдиагональную систему
трехдиагональную систему
с1 = 0
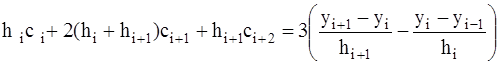 ,
,
cn+1 = 0,
которую решаем методом прогонки.
Для ai справедливо требование ai = yi-1 коэффициенты bi, di находят из формул:
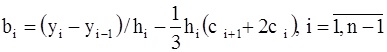 ,
,
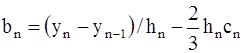 ,
,
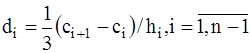 .
.
Для погрешности интерполяции справедлива оценка
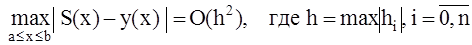 .
.
 2015-10-22
2015-10-22 473
473







