2015-10-22
2109
Интерполяция в общем понимании - это нахождение промежуточных значений величины по некоторым известным ее значениям.
Интерполяция применяется во многих задачах, связанных с вычислениями, например:
1) восстановить функцию y(x) для всех значений x на отрезке [a,b], если известны ее значения в некотором конечном числе точек этого отрезка;
2) заменить функцию близким выражением, удобным для проведения вычислений, если исходная функция представлена выражением, трудным для вычислений;
3) выполнить субтабулирование, т.е. сгущение таблицы значений;
4) решить задачу обратного интерполирования, т.е. по заданной таблице yi=y(xi) значений функции найти x как функцию от y.
В результате возникает следующая математическая задача: пусть на отрезке [a,b] задана сетка 
, в ее узлах заданы значения функций y(x), равные y(x0) = y0, y(x1) = y1, …, y(xi) = yi, …, y(xn) = yn. Требуется построить интерполянту, т.е. функцию j(x), совпадающую с функцией y(x) в узлах сетки
| j(xi) = yi, i = 0, 1, …, n. | (6.1) |
Интерполянта строится, как правило, в виде линейной комбинации некоторых линейно независимых на отрезке [a,b] элементарных функций
|
|
|
{jk(x)}, k = 0, 1, …, n;
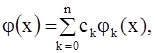| (6.2) |
где ck -неизвестные коэффициенты. Из условия (6.1) для определения этих коэффициентов получимсистему (n+1) уравнений
| (6.3) |
Система функций {jk(x)}, k = 0, 1, …, n такова, что при любом выборе сетки узлов 
отличен от нуля определитель системы (6.3)
Поэтому из системы (6.3) однозначно определяются коэффициенты ск.
В качестве функции j(x) в дальнейшем будем брать алгебраический многочлен степени n, т.е. j(x) = Pn(x). В этом случае интерполяция называется алгебраической. Алгебраическая интерполяция является наиболее распространенной, т.к. многочлены легко вычисляются, их легко дифференцировать и интегрировать. В этом случае в качестве системы линейно независимых функций {jk(x)} обычно выбирают следующую систему: jk(x) = xk, k = 0, 1, …, n.
Двух различных интерполяционных полиномов одной и той же степени n существовать не может. Действительно, предположив обратное, приходим к выводу, что разность двух таких многочленов, являющаяся многочленом степени не вышеn, имеет (n+1) корней, следовательно, равна тождественно нулю.
