Интерполяционный полином Ньютона

Пусть y₀ = y(x₀), y₁ = y(x₁), …, y_n = y(x_n) - значения функции y(x) в узлах интерполяции. Тогда разности

Dy₀ = y₁ – y₀, Dy₁ = y₂ – y₁, …, Dy_n-1 = y_n – y_n-1

называются конечными разностями первого порядка или просто первыми разностями.

Разностями второго порядка или вторыми разностями называются разности первых разностей, т.е.

D²y₀ = Dy₁ - Dy₀, D²y₁ = Dy₂ - Dy₁, …, D²y_n-2 = Dy_n-1 - Dy_n-2.

Аналогично определяются последующие разности. Например, разность (к+1)-го порядка получается из разности k-го порядка по формулам

D^k+1y₀ = D^ky₁ - D^ky₀, D^k+1y₁ = D^ky₂ - D^ky₁.

Разности высших порядков выражаются через y_i следующими формулами:

Введем так называемые разделенные разности.

Разделенные разности первого порядка определяются формулой

y(x_i, x_j) = (y_i – y_j) / (x_i – x_j).

Например,

y(x₁, x₀) = (y₁ – y₀)/(x₁ – x₀) = Dy₀/h₁, где h₁ = x₁ – x₀,

y(x₂, x₁) = (y₂ – y₁)/(x₂ – x₁) = Dy₁/h₂, где h₂ = x₂ – x₁, и т.д.

Разделенные разности второго порядка определяются формулой

y(x_i, x_j, x_k) = [y(x_i, x_j) – y(x_j, x_k)] / (x_i – x_k).

Разделенные разности k-го порядка определяются формулой

y(x_k, x_k-1, …, x₁, x₀) = [y(x_k, x_k-1, …, x₁) – y(x_k-1, …, x₀)] / (x_k – x₀).

В случае равностоящих узлов с шагом h для разделенных разностей имеем формулы:

y(x₁, x₀) = Dy₀ / h, y(x₂, x₁) = Dy₁ / h, …, y(x_n, x_n-1) = Dy_n-1 / h;

y(x₂, x₁, x₀) = D²y₀ / 2!h², y(x₃, x₂, x₁) = D²y₁ / 2!h, …;

y(x_k, x_k-1, x₀) = D^ky₀ / k!h.

Если у(x)=P_n(x) - полином степени n, то для него первая разделенная разность P(x, x₀) = (P(x) – P(x₀)) / (x – x₀) - есть полином степени (n-1), вторая разделенная разность P(x,x₀,x₁) - полином степени (n-2), так что разделенная разность (n+1)-го порядка равна нулю.

Разделенные разности располагаются по схеме:

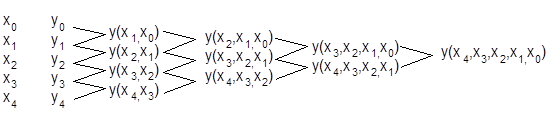
Рассмотрим первую разделенную разность для функции y(x)

y(x, x₀) = (y(x) – y₀) / (x – x₀), откуда y(x) = y₀ + (x – x₀) y(x, x₀).

Далее имеем

y(x, x₀) = y(x₀, x₁) + (x – x₁) y(x, x₀, x₁),

y(x, x₀, x₁) = y(x₀, x₁, x₂) + (x – x₂) y(x, x₂, x₁, x₀)

и т.д. Отсюда получаем формулу

y(x) = y₀ + (x – x₀) y(x₀, x₁) + (x – x₀) (x – x₁) y(x₀, x₁, x₂) + … +

+ (x – x₀) (x – x₁) … (x – x_n-1) y(x₀, x₁, …, x_n) +

+ (x – x₀) … (x – x_n) y(x, x₀, …, x_n)

или

y(x) = P_n(x) + (x – x₀) (x – x₁) … (x – x_n) y(x, x₀, x₁, …, x_n),

где

.

(6.10)

Если положить в формуле (6.10) x = x_k, k = 0, 1, …, n, получим P_n(x_k) = y_k.

Следовательно, полином (6.10) является интерполяционным полиномом, построенным по (n+1) узлам x₀, x₁,..., x_n. Он называется интерполяционным многочленом Ньютона.

В силу того, что любой k-й член полинома Ньютона (6.10) зависит только от к первых узлов интерполяции и от значений функции в этих узлах, добавление новых узлов вызывает лишь добавление в формуле (6.10) новых членов без изменения первоначальных, в этом состоит существенное, с точки зрения организации вычислений, преимущество полинома Ньютона по сравнению с полиномом Лагранжа.

Формулу для полинома Ньютона (6.10) можно переписать в следующем виде:

В данном случае базис состоит из функций вида

,

В этом случае c_k = y(x₀, x₁,..., x_k), После вычисления коэффициентов c_k, значения полинома Ньютона в точке x удобно вычислять по схеме Горнера

P_n(x) = y₀ + (x – x₀)[y(x₀, x₁) + (x - x₁)[y(x₀, x₁, x₂) + …]].

Вычисление значений x полинома P_n(x) (после вычисления c_k) требует n умножений и 2n сложений (или вычитаний), т.е. Q = 3n.

На практике избегают пользоваться интерполяционными многочленами высоких степеней. Объясняется это тем, что с ростом числа узлов сетки погрешность интерполирования f(x) – L_n(x) может не только не уменьшаться, но и в некоторых случаях постепенно расти с увеличением n. В этом случае говорят, что интерполяционный процесс расходится. Например, последовательность многочленов Ньютона, построенных для непрерывной функции f(x) = x на отрезке [-1, 1] не сходится к функции f(x) = x ни в одной точке отрезка [-1, 1] кроме точек –1, 0, 1. Поэтому более предпочтительной является интерполяция сплайнами, к рассмотрению которой мы переходим.